Confidence, Reliability, and Pattern Measurement: A Complete Information with Charts
Associated Articles: Confidence, Reliability, and Pattern Measurement: A Complete Information with Charts
Introduction
With enthusiasm, let’s navigate by the intriguing matter associated to Confidence, Reliability, and Pattern Measurement: A Complete Information with Charts. Let’s weave fascinating info and provide contemporary views to the readers.
Desk of Content material
Confidence, Reliability, and Pattern Measurement: A Complete Information with Charts
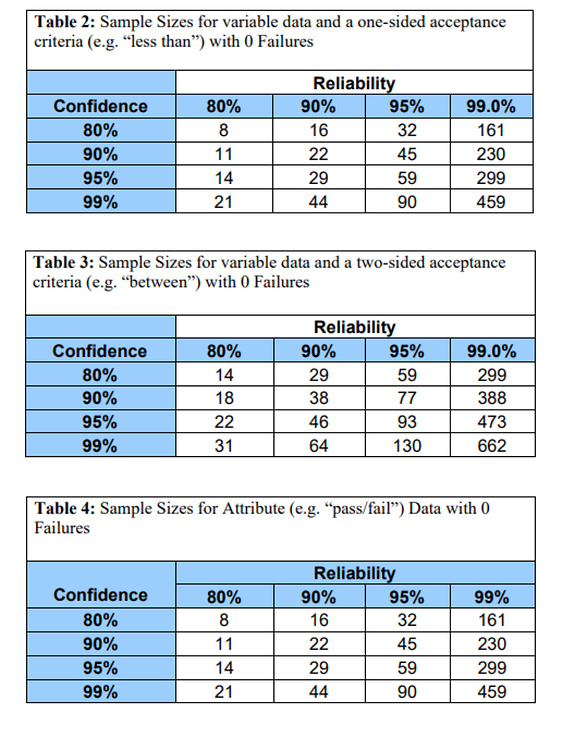
Figuring out the suitable pattern dimension for a analysis research is essential for making certain the reliability and validity of the outcomes. A pattern that is too small might result in inaccurate conclusions, whereas an excessively giant pattern may be expensive and inefficient. The best pattern dimension depends upon a number of elements, primarily the specified stage of confidence, the appropriate margin of error (or precision), and the anticipated variability inside the inhabitants. This text delves into the connection between these elements, explains easy methods to decide the suitable pattern dimension, and offers illustrative charts to information decision-making.
Understanding Key Ideas:
Earlier than exploring pattern dimension willpower, let’s make clear the core ideas:
-
Confidence Degree: This represents the chance that the true inhabitants parameter falls inside the calculated confidence interval. Frequent confidence ranges are 90%, 95%, and 99%. The next confidence stage implies a wider confidence interval, requiring a bigger pattern dimension. For instance, a 99% confidence stage means we’re 99% assured that the true inhabitants parameter lies inside our calculated vary.
-
Margin of Error (or Precision): That is the appropriate vary of error across the pattern statistic. It represents the utmost distinction between the pattern estimate and the true inhabitants parameter. A smaller margin of error calls for a bigger pattern dimension. For example, a margin of error of ±3% means we’re assured that the true worth lies inside 3 proportion factors of our pattern estimate.
-
Inhabitants Variability: This refers back to the unfold or dispersion of knowledge inside the inhabitants. Excessive variability necessitates a bigger pattern dimension to attain the specified precision. Variability is usually estimated utilizing the inhabitants normal deviation (σ) or the pattern normal deviation (s). If prior data in regards to the inhabitants variability is missing, a conservative estimate (e.g., assuming most variability) is usually used.
-
Pattern Measurement (n): That is the variety of people or objects chosen from the inhabitants for the research. The pattern dimension straight impacts the precision and reliability of the outcomes.
The Interaction of Confidence, Margin of Error, and Pattern Measurement:
The connection between these elements may be expressed mathematically, typically utilizing the next formulation (for estimating a inhabitants proportion):
n = (Z^2 * p * (1-p)) / E^2The place:
-
n= pattern dimension -
Z= Z-score equivalent to the specified confidence stage (e.g., 1.96 for 95% confidence) -
p= estimated proportion of the inhabitants possessing the attribute of curiosity (if unknown, use 0.5 for optimum variability) -
E= desired margin of error
This formulation highlights the direct relationship between the Z-score (confidence stage) and pattern dimension and the inverse relationship between the margin of error and pattern dimension. The next confidence stage or smaller margin of error will end in a bigger required pattern dimension.
Pattern Measurement Charts:
Whereas the formulation offers a exact calculation, pattern dimension charts provide a fast and intuitive technique to estimate the required pattern dimension. Beneath are simplified examples, keep in mind that these charts are for illustrative functions and should not cowl all situations. For extra advanced conditions, statistical software program or on-line calculators are beneficial.
(Chart 1: Pattern Measurement for Estimating Inhabitants Proportion with 95% Confidence)
| Margin of Error (%) | Estimated Proportion (p) = 0.1 | Estimated Proportion (p) = 0.3 | Estimated Proportion (p) = 0.5 |
|---|---|---|---|
| ± 5% | 271 | 601 | 960 |
| ± 3% | 676 | 1503 | 2401 |
| ± 1% | 9604 | 21609 | 34570 |
(Chart 2: Pattern Measurement for Estimating Inhabitants Imply with 95% Confidence)
This chart requires an estimate of the inhabitants normal deviation (σ).
| Margin of Error | Inhabitants Commonplace Deviation (σ) = 10 | Inhabitants Commonplace Deviation (σ) = 20 | Inhabitants Commonplace Deviation (σ) = 30 |
|---|---|---|---|
| ± 1 | 384 | 1537 | 3457 |
| ± 2 | 96 | 384 | 864 |
| ± 5 | 15 | 61 | 173 |
Notice: These charts assume a 95% confidence stage. Pattern sizes will enhance for greater confidence ranges.
Deciphering the Charts:
For example we’re conducting a survey to estimate the proportion of people that want a selected model of espresso. We would like a 95% confidence stage and a margin of error of ±3%. If we estimate that roughly 30% of the inhabitants prefers this model (p=0.3), Chart 1 signifies we’d like a pattern dimension of roughly 1503 people.
If we’re measuring a steady variable like top, and we all know the inhabitants normal deviation is roughly 10 (σ=10), and we would like a margin of error of ±2, Chart 2 suggests a pattern dimension of 96 people is adequate.
Limitations of Pattern Measurement Charts:
-
Simplified Assumptions: These charts typically make simplifying assumptions in regards to the inhabitants distribution (e.g., normality). Actual-world information might not completely meet these assumptions.
-
Lack of Context: The charts don’t account for elements resembling stratification, clustering, or non-response bias, which might considerably have an effect on the required pattern dimension.
-
Restricted Scope: They usually deal with easy situations and will not be appropriate for extra advanced analysis designs.
Superior Concerns:
-
Finite Inhabitants Correction: When the pattern dimension is a big proportion of the overall inhabitants, a finite inhabitants correction issue needs to be utilized to regulate the pattern dimension calculation.
-
Energy Evaluation: For speculation testing, energy evaluation is essential to find out the pattern dimension wanted to detect a statistically vital impact with a specified energy stage.
-
Statistical Software program: Software program packages like SPSS, R, and SAS provide subtle instruments for calculating pattern sizes based mostly on varied analysis designs and statistical checks.
Conclusion:
Selecting the best pattern dimension is important for making certain the reliability and validity of analysis findings. Whereas pattern dimension charts present a helpful start line, they need to be used judiciously. An intensive understanding of confidence ranges, margins of error, inhabitants variability, and potential biases is important for figuring out an acceptable pattern dimension. For advanced research or when excessive precision is required, consulting with a statistician is very beneficial. Keep in mind that a well-designed research with a fastidiously decided pattern dimension is the muse for producing credible and impactful analysis outcomes.




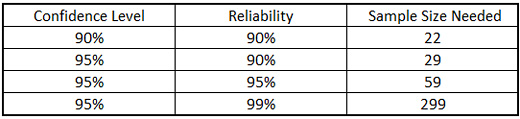
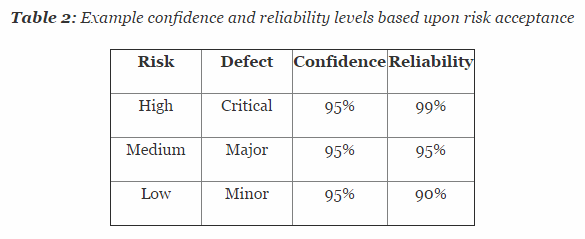

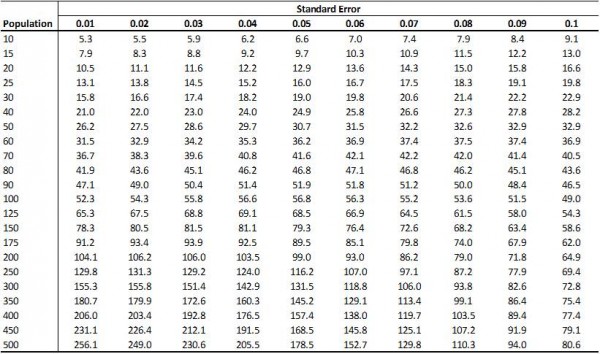
Closure
Thus, we hope this text has offered precious insights into Confidence, Reliability, and Pattern Measurement: A Complete Information with Charts. We hope you discover this text informative and helpful. See you in our subsequent article!