Decoding The Commonplace Regular Distribution Z-Desk: A Complete Information

Decoding the Commonplace Regular Distribution Z-Desk: A Complete Information

Associated Articles: Decoding the Commonplace Regular Distribution Z-Desk: A Complete Information

Introduction

With nice pleasure, we are going to discover the intriguing subject associated to Decoding the Commonplace Regular Distribution Z-Desk: A Complete Information. Let’s weave attention-grabbing info and provide contemporary views to the readers.

Decoding the Commonplace Regular Distribution Z-Desk: A Complete Information

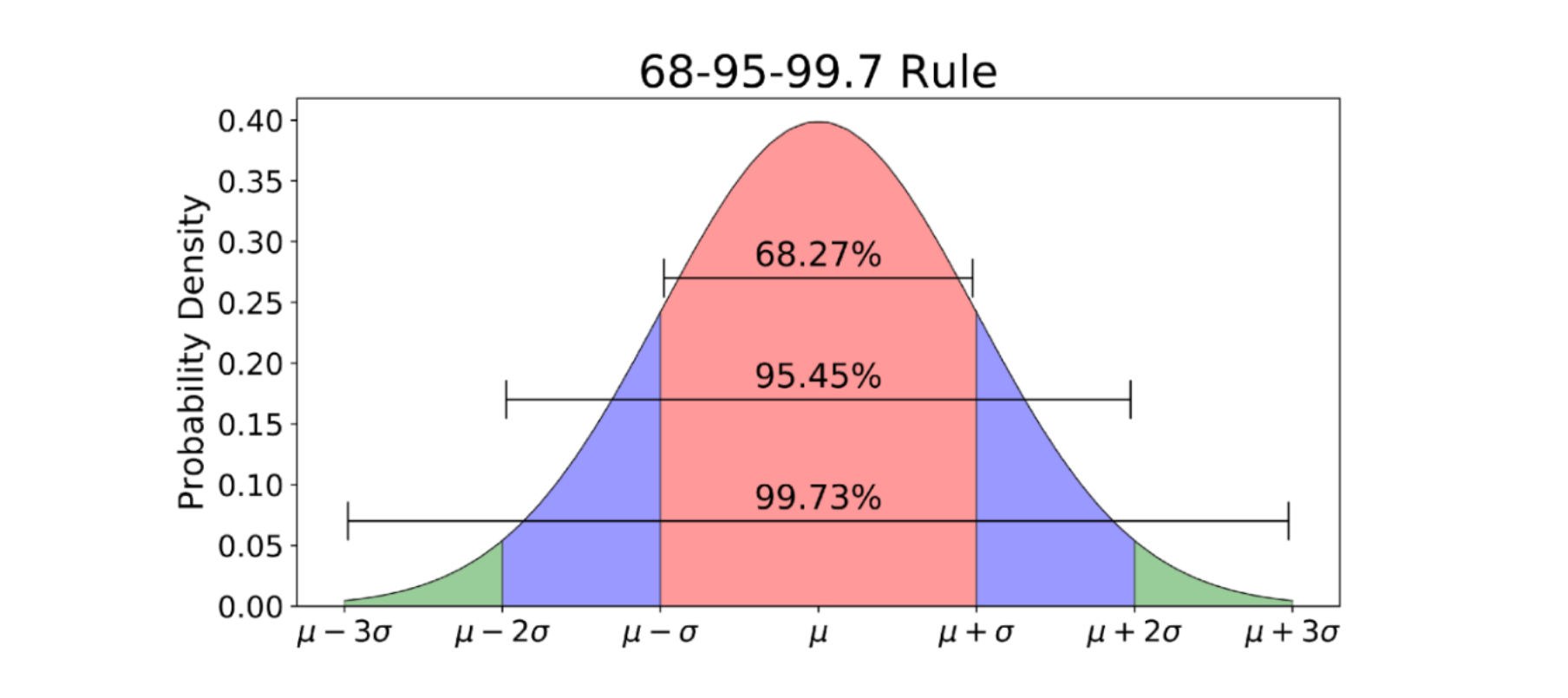
The usual regular distribution, typically represented by the letter Z, is a cornerstone of statistical evaluation. It is a particular kind of regular distribution with a imply (μ) of 0 and a typical deviation (σ) of 1. Understanding this distribution is essential for a variety of purposes, from speculation testing and confidence intervals to calculating possibilities related to varied phenomena. Central to this understanding is the Z-table, an important instrument that permits us to find out possibilities related to particular Z-scores. This text supplies a complete exploration of the Z-table, its development, interpretation, and sensible purposes.

Understanding the Commonplace Regular Distribution

Earlier than diving into the Z-table, it is important to understand the basic traits of the usual regular distribution. Its bell-shaped curve is completely symmetrical across the imply of 0. Which means that 50% of the info lies beneath the imply, and 50% lies above it. The usual deviation of 1 supplies a standardized unit of measurement, enabling straightforward comparability throughout totally different datasets. The world beneath the curve represents chance; the overall space beneath the curve equals 1 (or 100%).

The Z-score, or Z-value, represents the variety of commonplace deviations a selected knowledge level is away from the imply. A constructive Z-score signifies the info level is above the imply, whereas a adverse Z-score signifies it is beneath the imply. For instance, a Z-score of 1.5 means the info level is 1.5 commonplace deviations above the imply.

The Development of the Z-Desk

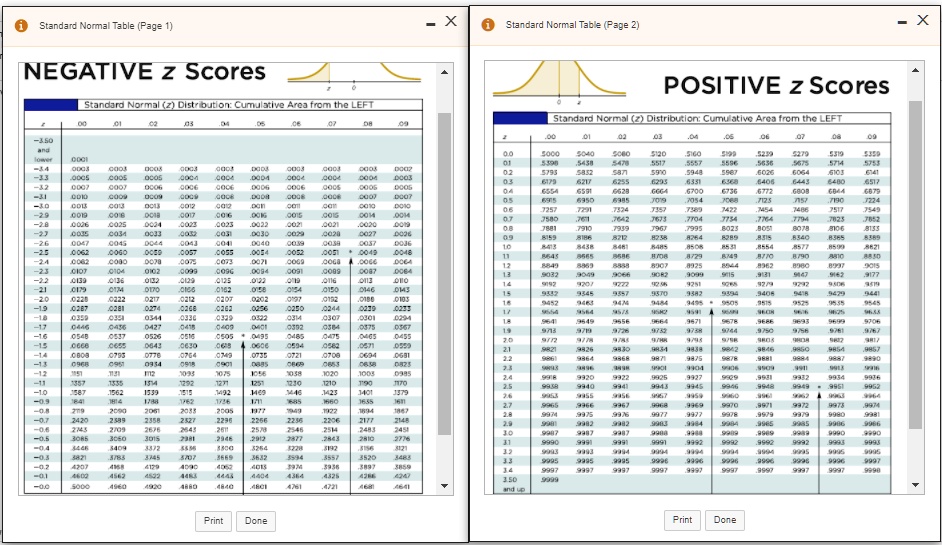
The Z-table, also called the usual regular desk or unit regular desk, is a tabular illustration of the cumulative chance distribution operate (CDF) of the usual regular distribution. It supplies the chance {that a} randomly chosen worth from the usual regular distribution might be lower than or equal to a given Z-score. The desk is often organized in two components:

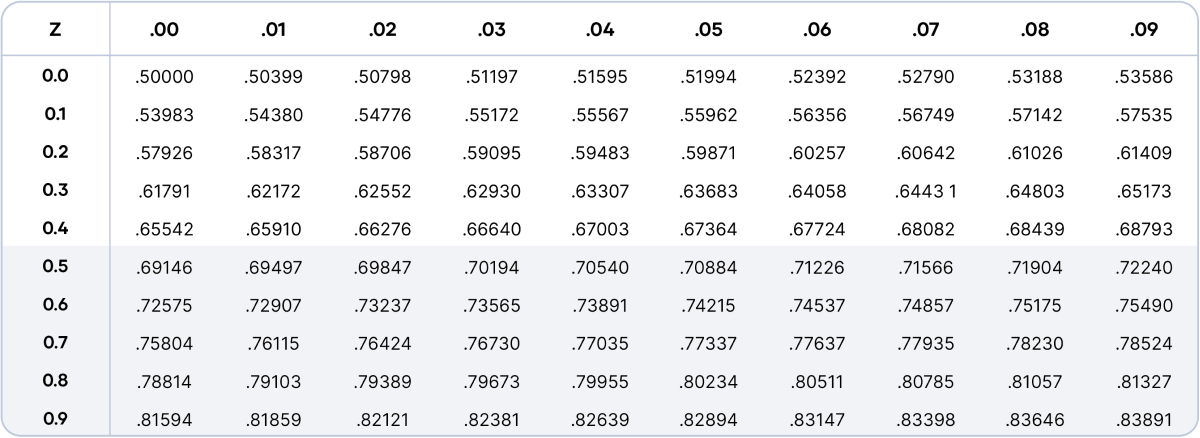
• The Physique of the Desk: This part accommodates the chances. Every cell represents the chance P(Z ≤ z), the place ‘z’ is the Z-score. The Z-score is often introduced to 2 decimal locations. The primary decimal place is discovered within the leftmost column, and the second decimal place is discovered within the high row. The intersection of the row and column supplies the corresponding chance.

• The Tails of the Distribution: Whereas the physique of the desk focuses on the cumulative chance from adverse infinity as much as a selected Z-score, it is essential to grasp learn how to calculate possibilities within the tails of the distribution. These symbolize possibilities of utmost values.

Deciphering the Z-Desk

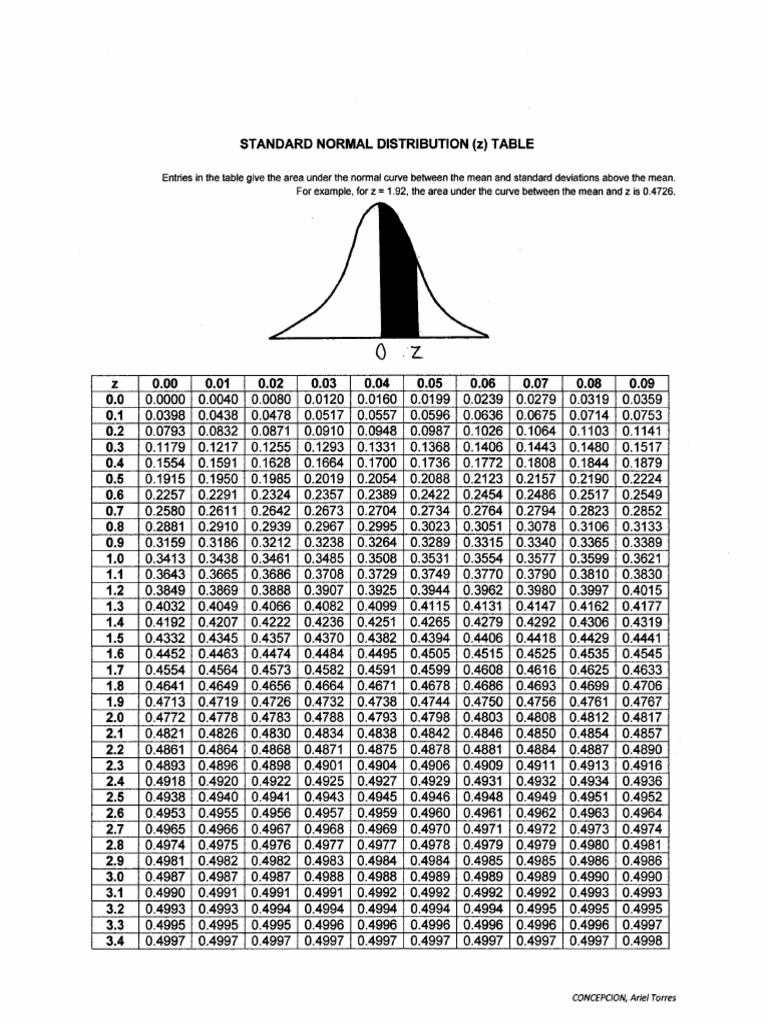
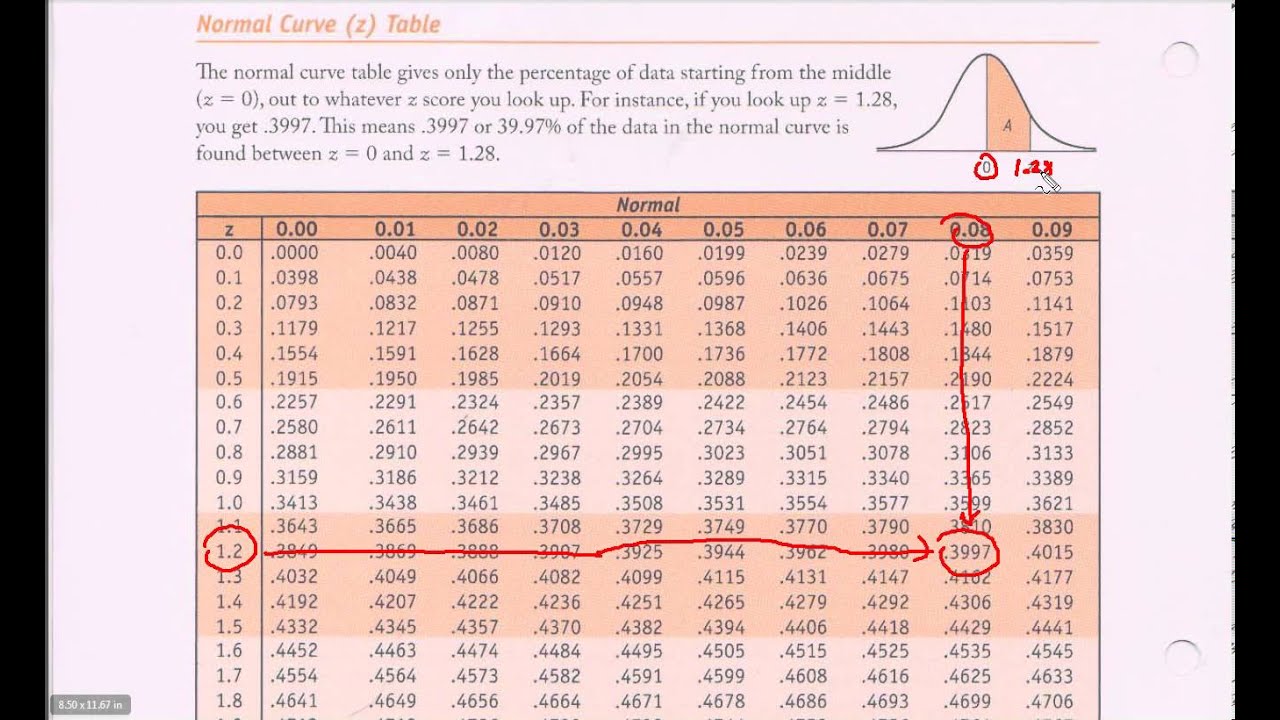
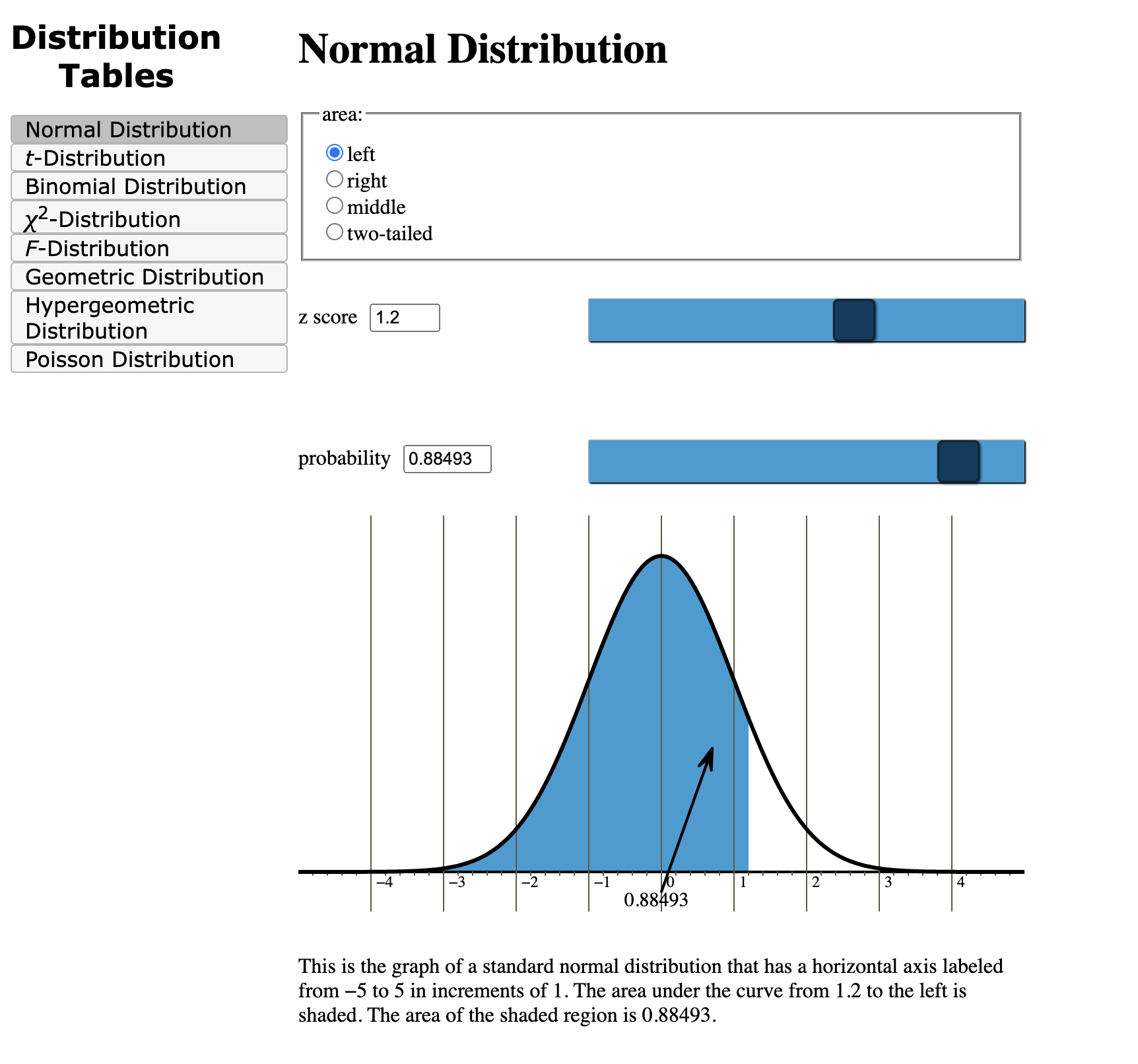
Let’s illustrate with an instance. Suppose we need to discover the chance {that a} randomly chosen worth from the usual regular distribution is lower than or equal to 1.96 (Z ≤ 1.96). We find 1.9 within the leftmost column and 0.06 within the high row. The intersection of this row and column offers us a chance of roughly 0.9750. This implies there is a 97.5% probability {that a} randomly chosen worth might be lower than or equal to 1.96 commonplace deviations above the imply.

Conversely, if we need to discover the chance that Z is bigger than 1.96 (Z > 1.96), we use the complement rule: P(Z > 1.96) = 1 – P(Z ≤ 1.96) = 1 – 0.9750 = 0.0250. This implies there is a 2.5% probability {that a} randomly chosen worth might be better than 1.96 commonplace deviations above the imply.

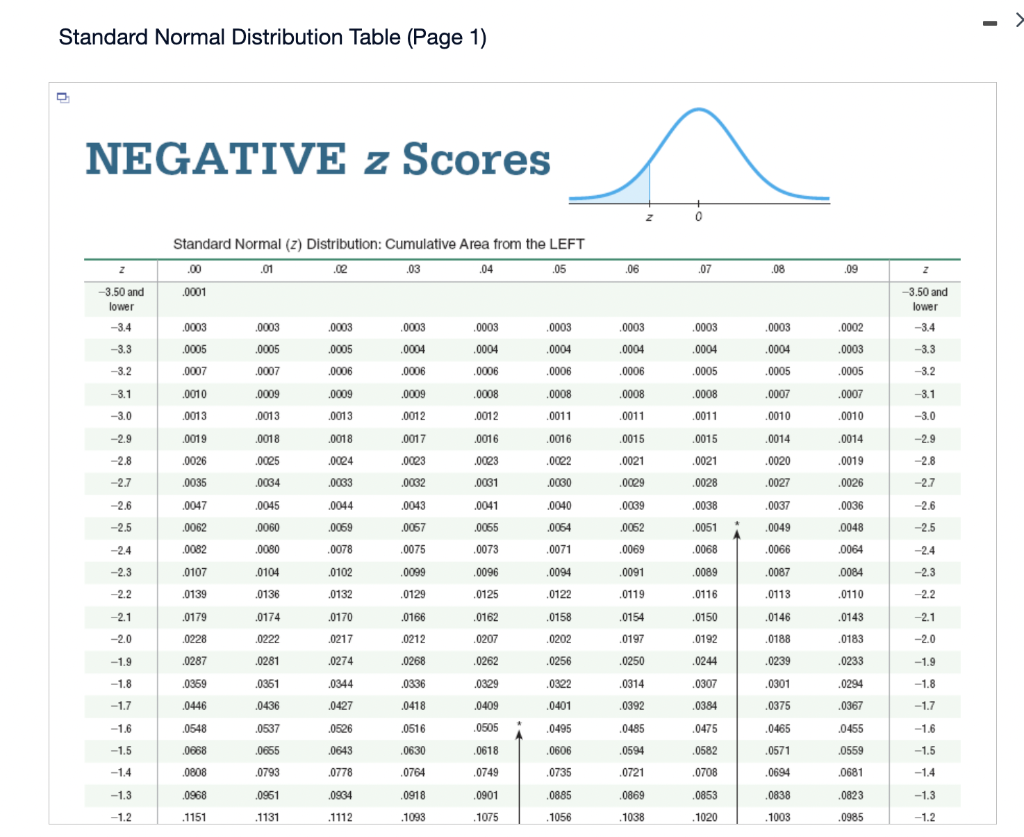
For adverse Z-scores, the method is analogous. The desk supplies possibilities for adverse Z-scores immediately. For example, to search out P(Z ≤ -1.96), we find -1.9 within the leftmost column and 0.06 within the high row. The corresponding chance is roughly 0.0250. Notice the symmetry: P(Z ≤ -1.96) = P(Z ≥ 1.96).

Purposes of the Z-Desk

The Z-table is an indispensable instrument in varied statistical contexts:

• Speculation Testing: Many speculation checks contain evaluating a check statistic to a essential worth obtained from the Z-table. This helps decide whether or not to reject or fail to reject the null speculation.

• Confidence Intervals: Setting up confidence intervals for inhabitants means or proportions typically depends on the Z-table to search out the essential Z-value equivalent to the specified confidence stage.

• Chance Calculations: The Z-table permits us to calculate possibilities related to particular ranges of values in a usually distributed dataset. That is significantly helpful when coping with steady knowledge.

• Percentile Calculations: We will decide the Z-score equivalent to a selected percentile utilizing the Z-table. For instance, the Z-score equivalent to the ninety fifth percentile is roughly 1.645.

• Information Standardization and Comparability: The Z-score, calculated utilizing the Z-table, permits us to standardize knowledge from totally different distributions, making them comparable.

Limitations of the Z-Desk

Whereas the Z-table is a strong instrument, it has limitations:

• Accuracy: The Z-table supplies possibilities to a restricted variety of decimal locations. Extra exact calculations could require statistical software program.

• Interpolation: When the specified Z-score shouldn’t be immediately accessible within the desk, interpolation is important, which introduces a small diploma of approximation.

• Non-Regular Distributions: The Z-table is barely relevant to knowledge that follows a typical regular distribution. For different distributions, totally different strategies are required.

Options to the Z-Desk

With the appearance of superior statistical software program and calculators, various strategies for calculating possibilities related to the usual regular distribution are available. Software program packages like R, SPSS, SAS, and Python’s SciPy library provide capabilities that present extremely correct possibilities for any Z-score. Many scientific calculators even have built-in capabilities for calculating these possibilities. These options typically provide better precision and eradicate the necessity for interpolation.

Conclusion

The Z-table is a elementary instrument for anybody working with statistical knowledge. Its means to supply possibilities related to Z-scores underpins many essential statistical procedures. Whereas various strategies can be found, understanding the Z-table and its interpretation stays important for greedy the underlying ideas of statistical evaluation. By mastering using the Z-table, one features a deeper understanding of the usual regular distribution and its software in a wide selection of statistical issues, from easy chance calculations to advanced speculation testing situations. The mixture of theoretical understanding and sensible software of the Z-table is vital to unlocking the facility of statistical inference.

Closure

Thus, we hope this text has offered invaluable insights into Decoding the Commonplace Regular Distribution Z-Desk: A Complete Information. We thanks for taking the time to learn this text. See you in our subsequent article!