Decoding The T-Distribution Chart: A Complete Information With Sensible Purposes

Decoding the t-Distribution Chart: A Complete Information with Sensible Purposes

Associated Articles: Decoding the t-Distribution Chart: A Complete Information with Sensible Purposes

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the t-Distribution Chart: A Complete Information with Sensible Purposes. Let’s weave fascinating info and provide recent views to the readers.

Decoding the t-Distribution Chart: A Complete Information with Sensible Purposes

The t-distribution, a cornerstone of inferential statistics, performs a vital function in speculation testing and confidence interval estimation, notably when coping with small pattern sizes or unknown inhabitants commonplace deviations. In contrast to the traditional distribution, which depends on understanding the inhabitants parameters, the t-distribution gives a strong various, offering correct estimations even with restricted knowledge. Understanding the t-distribution chart (usually introduced as a PDF desk) is due to this fact important for anybody working with statistical evaluation. This text offers a complete information to deciphering and using t-distribution charts, accompanied by sensible examples and explanations.

Understanding the t-Distribution

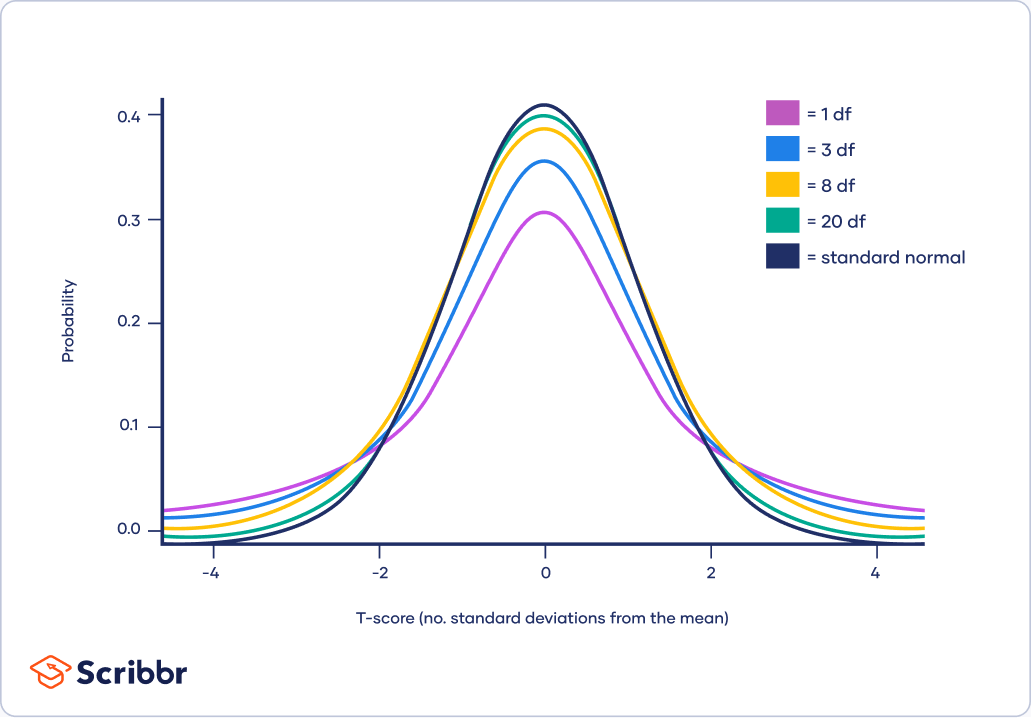
The t-distribution, also referred to as Scholar’s t-distribution (named after William Sealy Gosset, who revealed below the pseudonym "Scholar"), is a household of likelihood distributions. In contrast to the traditional distribution, which has a single form, the t-distribution’s form varies relying on a parameter referred to as the levels of freedom (df). The levels of freedom are associated to the pattern dimension (n) and are usually calculated as df = n – 1.

Because the levels of freedom enhance, the t-distribution steadily approaches the traditional distribution. With a big pattern dimension (and consequently, excessive levels of freedom), the distinction between the t-distribution and the traditional distribution turns into negligible. Nonetheless, with small pattern sizes, the t-distribution has heavier tails than the traditional distribution, reflecting the elevated uncertainty related to restricted knowledge. Which means there is a larger likelihood of observing excessive values within the t-distribution in comparison with the traditional distribution, particularly when the df is low.

The t-Distribution Chart (PDF)

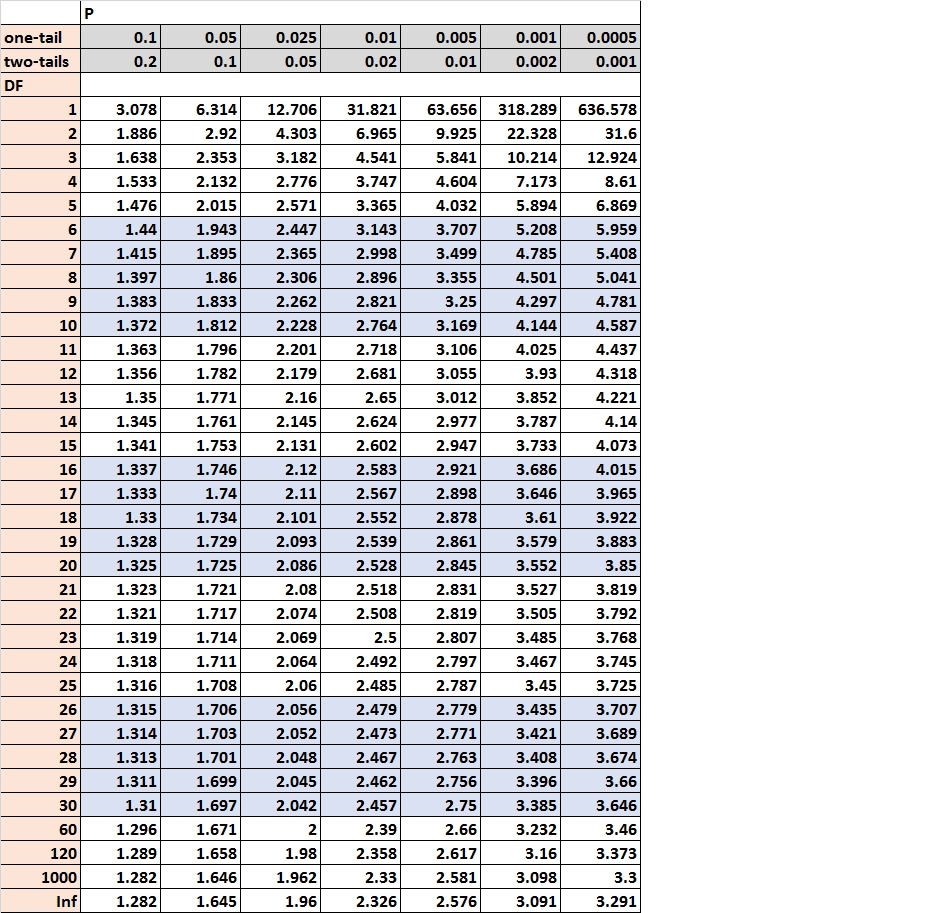
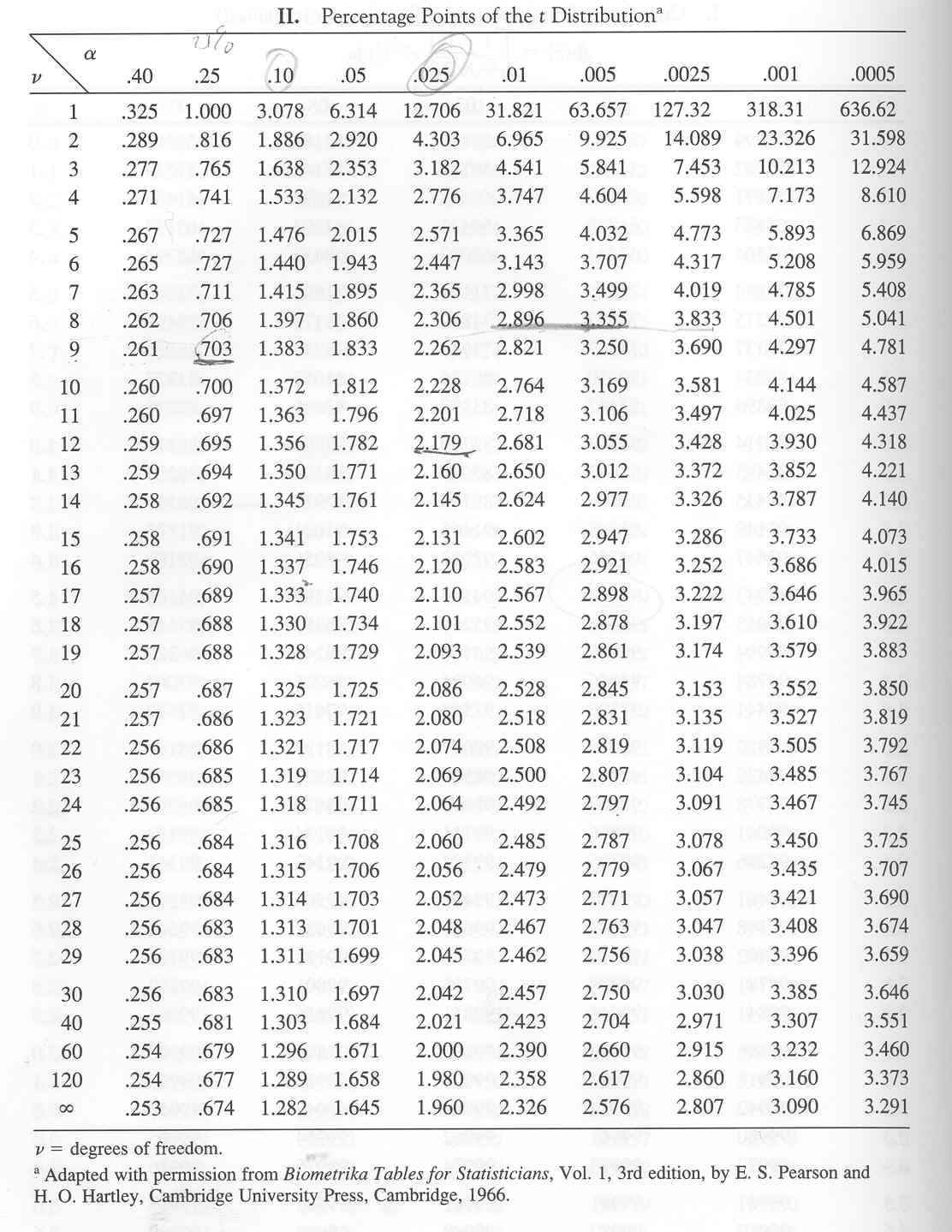
The t-distribution chart, normally introduced as a PDF, is a desk that gives crucial t-values for varied ranges of significance (alpha) and levels of freedom. These crucial t-values signify the boundaries of the rejection areas in speculation testing. The chart usually organizes this info in a matrix format:

• Rows: Symbolize the levels of freedom (df). The values usually vary from 1 to infinity (or a big quantity representing a near-normal distribution).
• Columns: Symbolize the alpha degree (significance degree), which is the likelihood of rejecting the null speculation when it’s truly true (Sort I error). Frequent alpha ranges are 0.10, 0.05, 0.025, 0.01, and 0.005, representing 10%, 5%, 2.5%, 1%, and 0.5% significance ranges respectively. These values correspond to one-tailed or two-tailed checks. A one-tailed take a look at focuses on one finish of the distribution (both the higher or decrease tail), whereas a two-tailed take a look at considers each tails.
• Cell Values: The intersection of a row (df) and a column (alpha) offers the crucial t-value. That is the worth {that a} calculated t-statistic should exceed (in absolute worth for a two-tailed take a look at) to reject the null speculation on the specified alpha degree.

Decoding the t-Distribution Chart

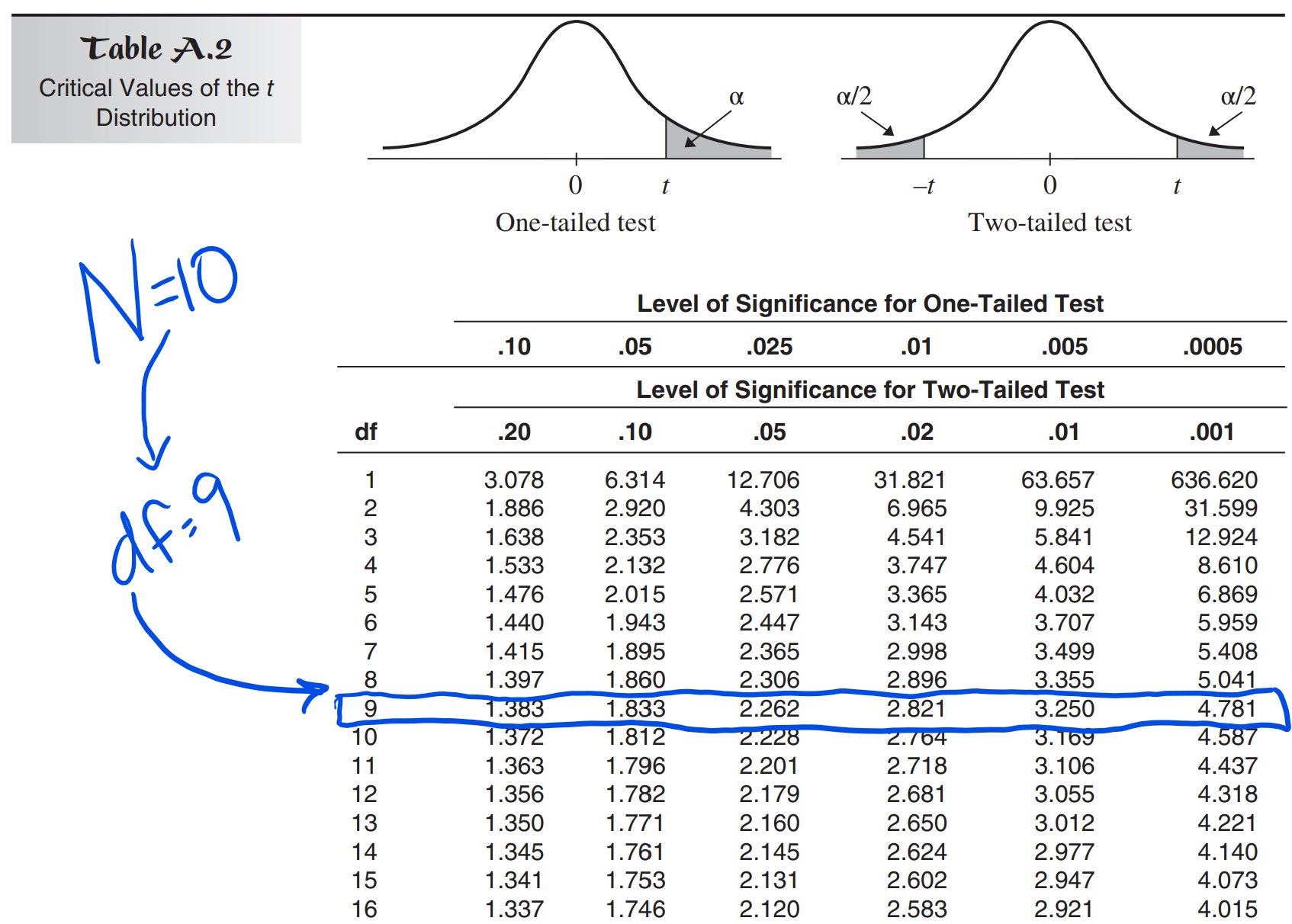
Let’s illustrate interpret a t-distribution chart with an instance. Suppose we’ve got a pattern dimension of 10 (n=10), leading to 9 levels of freedom (df=9). We wish to conduct a two-tailed speculation take a look at at a 5% significance degree (alpha = 0.05).

1. Find the levels of freedom: Discover the row equivalent to df = 9.
2. Find the alpha degree: Discover the column equivalent to alpha = 0.05 (two-tailed). Observe that some tables would possibly checklist this as alpha/2 = 0.025 for two-tailed checks.
3. Discover the crucial t-value: The cell the place the row (df=9) and column (alpha=0.05 two-tailed) intersect will present the crucial t-value. Let’s assume this worth is roughly 2.262.

Which means if our calculated t-statistic (obtained from our pattern knowledge) is larger than 2.262 or lower than -2.262, we’d reject the null speculation on the 5% significance degree.

Sensible Purposes of the t-Distribution Chart

The t-distribution chart is indispensable in varied statistical analyses:

• One-Pattern t-test: Used to check the imply of a pattern to a identified inhabitants imply when the inhabitants commonplace deviation is unknown.
• Two-Pattern t-test (Unbiased Samples): Used to check the technique of two unbiased teams.
• Paired t-test: Used to check the technique of two associated teams (e.g., earlier than and after measurements on the identical people).
• Confidence Interval Estimation: Used to assemble confidence intervals for inhabitants means when the inhabitants commonplace deviation is unknown. The crucial t-value from the chart is used to calculate the margin of error.

Instance: One-Pattern t-test

For example a researcher desires to check if the common peak of scholars in a university is completely different from the nationwide common of 68 inches. A pattern of 25 college students is taken, yielding a pattern imply of 70 inches and a pattern commonplace deviation of 4 inches.

1. State the hypotheses:

   • Null speculation (H0): The common peak is the same as 68 inches.
   • Different speculation (H1): The common peak will not be equal to 68 inches (two-tailed take a look at).

2. Calculate the t-statistic: Utilizing the system for a one-sample t-test, the t-statistic is calculated.

3. Decide the levels of freedom: df = n – 1 = 25 – 1 = 24.

4. Discover the crucial t-value: Utilizing the t-distribution chart with df = 24 and alpha = 0.05 (two-tailed), we discover the crucial t-value.

5. Decide: If the calculated t-statistic falls outdoors the vary outlined by the crucial t-values, we reject the null speculation. In any other case, we fail to reject the null speculation.

Limitations and Concerns

Whereas the t-distribution is a robust device, it is essential to recollect its limitations:

• Assumption of Normality: The t-tests assume that the information is roughly usually distributed. For small pattern sizes, deviations from normality can have an effect on the accuracy of the outcomes. Assessments for normality (e.g., Shapiro-Wilk take a look at) needs to be carried out.
• Independence of Observations: Observations throughout the pattern needs to be unbiased of one another.
• Homogeneity of Variances (for two-sample t-tests): The variances of the 2 teams being in contrast needs to be roughly equal. Assessments like Levene’s take a look at can assess this assumption.
• Outliers: Outliers can considerably affect the outcomes of t-tests. Figuring out and addressing outliers is essential.

Conclusion

The t-distribution chart is a necessary useful resource for anybody working with statistical evaluation involving small pattern sizes or unknown inhabitants commonplace deviations. By understanding interpret the chart and making use of the suitable t-tests, researchers could make knowledgeable choices primarily based on their knowledge. Nonetheless, it is vital to recollect the assumptions underlying the t-distribution and to think about potential limitations when deciphering outcomes. All the time accompany t-test outcomes with a dialogue of the assumptions and potential limitations to make sure a strong and dependable evaluation. The provision of readily accessible t-distribution charts in PDF format makes this highly effective statistical device simply accessible for a variety of functions. Understanding its nuances and limitations is essential to its efficient and accountable use.

Closure

Thus, we hope this text has offered helpful insights into Decoding the t-Distribution Chart: A Complete Information with Sensible Purposes. We thanks for taking the time to learn this text. See you in our subsequent article!