Decoding The T-Desk: A Complete Information To Pupil’s T-Distribution

Decoding the t-Desk: A Complete Information to Pupil’s t-Distribution

Associated Articles: Decoding the t-Desk: A Complete Information to Pupil’s t-Distribution

Introduction

With enthusiasm, let’s navigate by way of the intriguing matter associated to Decoding the t-Desk: A Complete Information to Pupil’s t-Distribution. Let’s weave attention-grabbing data and supply contemporary views to the readers.

Decoding the t-Desk: A Complete Information to Pupil’s t-Distribution

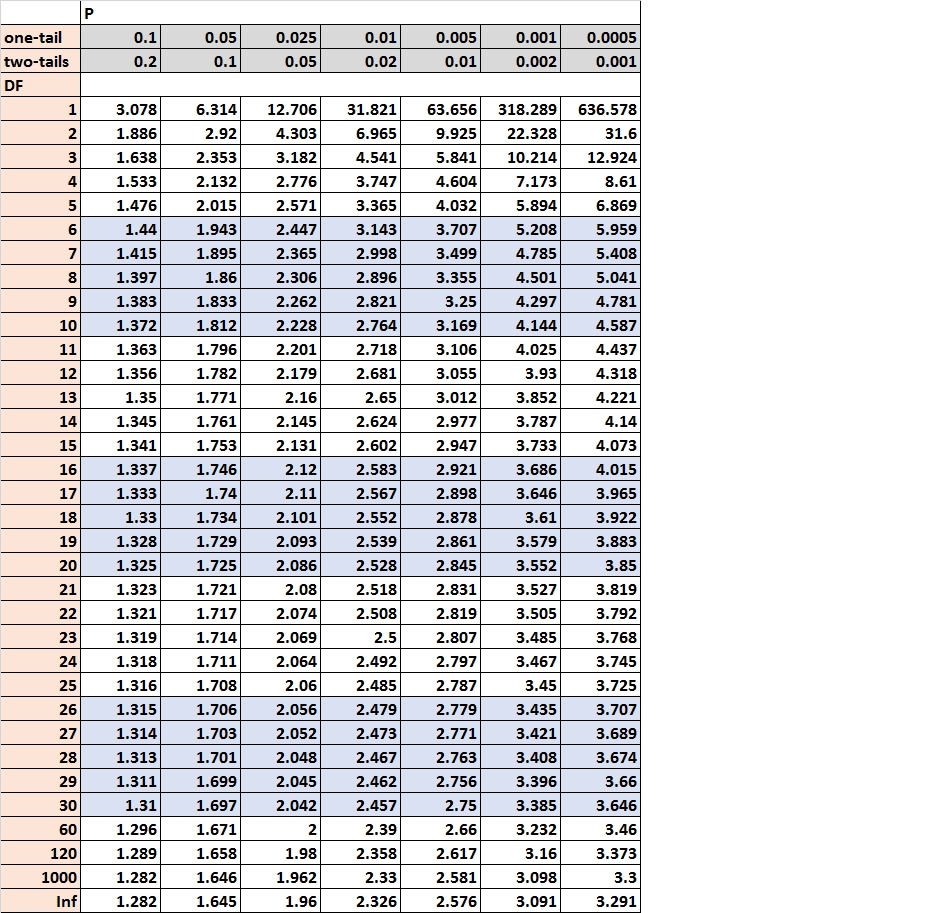
The t-table, a cornerstone of statistical inference, is a vital device for researchers and analysts alike. It supplies important values for Pupil’s t-distribution, a chance distribution used extensively in speculation testing and confidence interval estimation, notably when coping with small pattern sizes or unknown inhabitants normal deviations. Understanding the t-table and its purposes is crucial for deciphering statistical outcomes precisely and drawing significant conclusions from information. This text will delve into the intricacies of the t-table, explaining its construction, utilization, and the underlying ideas of the t-distribution.

Understanding Pupil’s t-Distribution

In contrast to the conventional distribution, which depends on realizing the inhabitants normal deviation, the t-distribution makes use of the pattern normal deviation as an estimate. That is essential as a result of, in lots of real-world eventualities, the inhabitants normal deviation is unknown. The t-distribution, developed by William Sealy Gosset (who printed below the pseudonym "Pupil"), accounts for the extra uncertainty launched by estimating the usual deviation from the pattern.

The form of the t-distribution is just like the conventional distribution – bell-shaped and symmetrical round its imply of zero. Nevertheless, it has heavier tails, which means it has the next chance of observing excessive values in comparison with the conventional distribution. This distinction is especially pronounced with smaller pattern sizes. Because the pattern dimension will increase, the t-distribution approaches the conventional distribution, ultimately changing into indistinguishable from it for giant pattern sizes (typically thought of to be above 30).

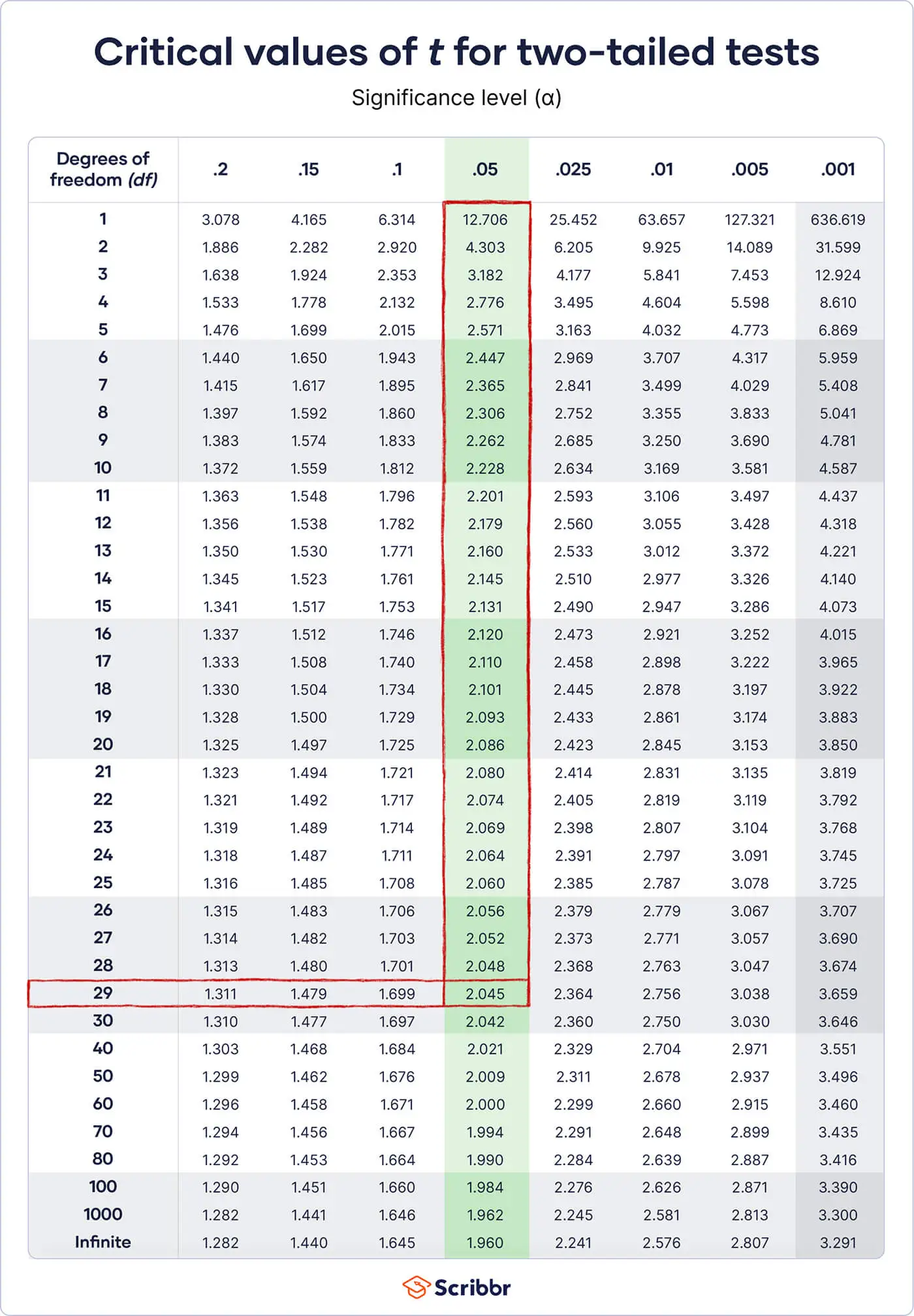
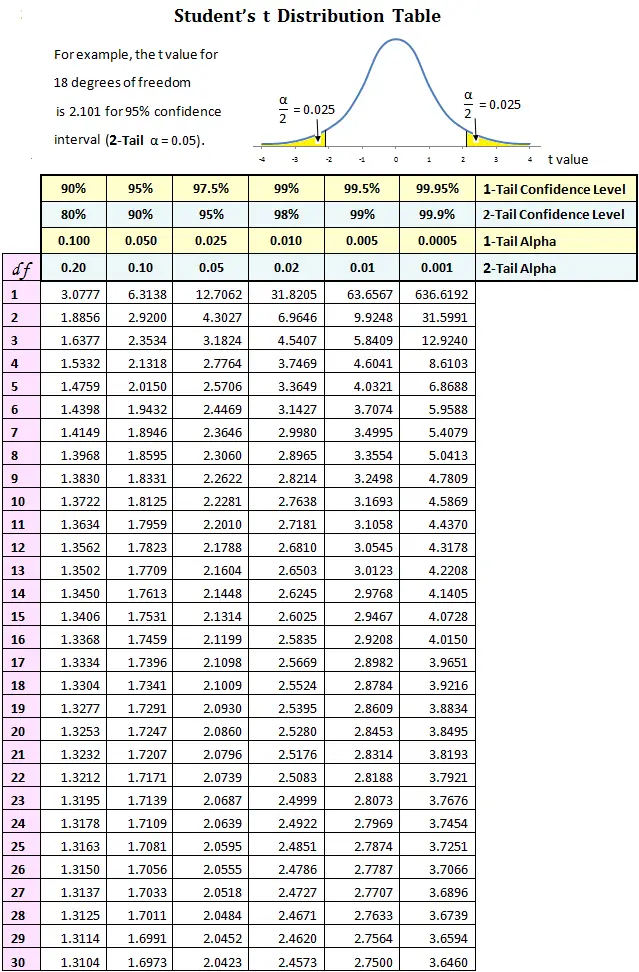
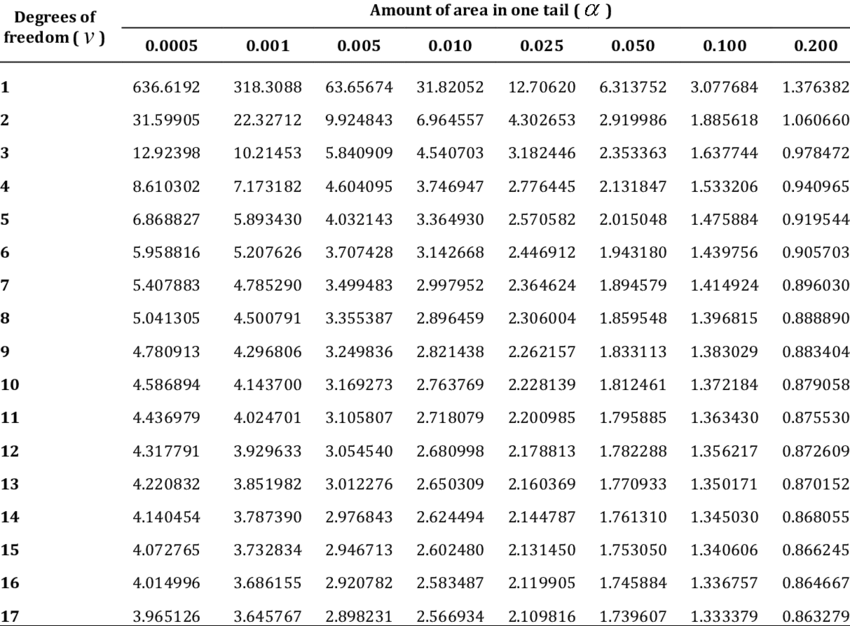
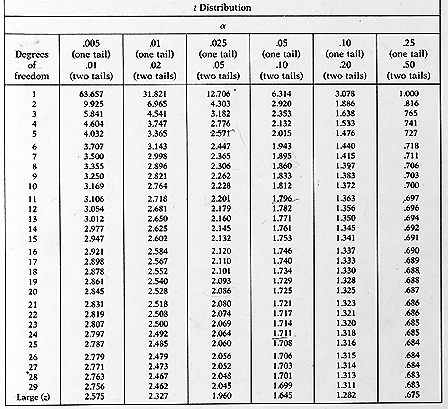
The Construction of the t-Desk

A typical t-table is organized in a tabular format, with rows representing levels of freedom (df) and columns representing totally different significance ranges (alpha ranges) or confidence ranges.

• Levels of Freedom (df): This represents the variety of unbiased items of data obtainable to estimate a parameter. In lots of widespread purposes, the levels of freedom are calculated as n – 1, the place n is the pattern dimension. The t-table usually lists levels of freedom from 1 to infinity. Because the levels of freedom enhance, the important t-value decreases, approaching the corresponding z-value from the usual regular distribution.

• Significance Degree (α): That is the chance of rejecting the null speculation when it’s truly true (Sort I error). Widespread significance ranges embody 0.10, 0.05, 0.025, 0.01, and 0.005. These values correspond to one-tailed assessments. For 2-tailed assessments, the importance degree is split by two (e.g., 0.05 turns into 0.025 for a two-tailed check on the 5% significance degree).

• Confidence Degree: This represents the chance that the true inhabitants parameter lies inside the confidence interval. It is the same as 1 – α. For instance, a 95% confidence degree corresponds to a significance degree of 0.05.

Utilizing the t-Desk for Speculation Testing

The t-table is instrumental in conducting speculation assessments involving the t-statistic. The t-statistic is calculated as:

t = (pattern imply – inhabitants imply) / (pattern normal deviation / √pattern dimension)

1. Decide the levels of freedom: Calculate the levels of freedom (df = n – 1).

2. Select the importance degree (α): Choose the suitable significance degree based mostly on the context of the speculation check (e.g., 0.05 for a 5% significance degree). Decide if it is a one-tailed or two-tailed check.

3. Find the important t-value: Discover the intersection of the row equivalent to your levels of freedom and the column equivalent to your chosen significance degree (or half of it for a two-tailed check). This worth is the important t-value.

4. Evaluate the calculated t-statistic to the important t-value:

   • If absolutely the worth of the calculated t-statistic is larger than the important t-value: Reject the null speculation. There’s ample proof to help the choice speculation.
   • If absolutely the worth of the calculated t-statistic is lower than or equal to the important t-value: Fail to reject the null speculation. There’s not sufficient proof to help the choice speculation.

Utilizing the t-Desk for Confidence Interval Estimation

The t-table can be essential in establishing confidence intervals. A confidence interval supplies a variety of values inside which the true inhabitants parameter is more likely to fall with a sure degree of confidence.

1. Decide the levels of freedom: Calculate the levels of freedom (df = n – 1).

2. Select the boldness degree: Choose the specified confidence degree (e.g., 95%). This corresponds to a significance degree of α = 1 – confidence degree (e.g., α = 0.05 for a 95% confidence degree).

3. Find the important t-value: Discover the intersection of the row equivalent to your levels of freedom and the column equivalent to α/2 (for a two-tailed confidence interval).

4. Calculate the margin of error: Multiply the important t-value by the usual error of the imply (pattern normal deviation / √pattern dimension).

5. Assemble the boldness interval: The arrogance interval is given by:

Pattern imply ± margin of error

Deciphering the Outcomes

The outcomes obtained utilizing the t-table ought to be interpreted inside the context of the analysis query and the constraints of the research. Do not forget that statistical significance doesn’t essentially indicate sensible significance. A statistically important outcome may need a small impact dimension that isn’t virtually related. Moreover, the assumptions underlying the t-test (e.g., normality, independence of observations) ought to be checked earlier than deciphering the outcomes.

Limitations of the t-Desk

Whereas the t-table is a strong device, it has limitations:

• Assumption of normality: The t-test is most correct when the information is often distributed. For severely non-normal information, non-parametric alternate options ought to be thought of.

• Small pattern sizes: The t-distribution’s heavier tails in comparison with the conventional distribution are notably noticeable with small pattern sizes. With very small samples, the t-test might lack energy.

• Dependence of observations: The t-test assumes that observations are unbiased. Violation of this assumption can result in inaccurate outcomes.

Software program Options

Whereas t-tables are available, statistical software program packages (like R, SPSS, SAS, and Python with libraries like SciPy) present extra environment friendly methods to carry out t-tests and calculate confidence intervals. These packages can deal with bigger datasets and supply extra complete output, together with p-values, which aren’t instantly obtainable in a normal t-table. Nevertheless, understanding the t-table stays essential for greedy the elemental ideas underlying these statistical procedures.

In conclusion, the t-table is a useful useful resource for conducting speculation assessments and establishing confidence intervals when coping with small pattern sizes or unknown inhabitants normal deviations. Understanding its construction, utilization, and limitations is crucial for appropriately deciphering statistical outcomes and making knowledgeable choices based mostly on information evaluation. Whereas software program packages supply extra environment friendly computations, a strong grasp of the t-table’s ideas stays elementary to a radical understanding of statistical inference.

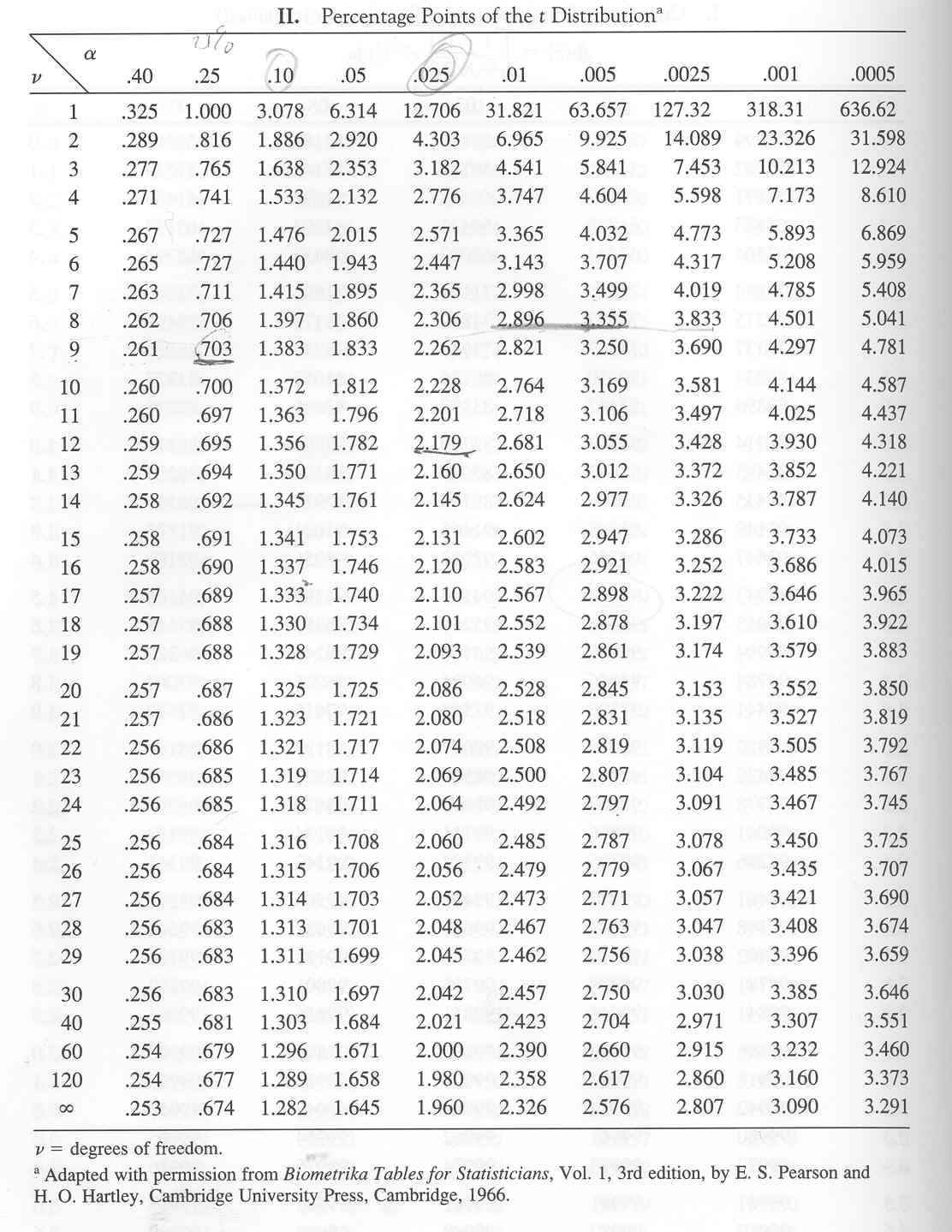
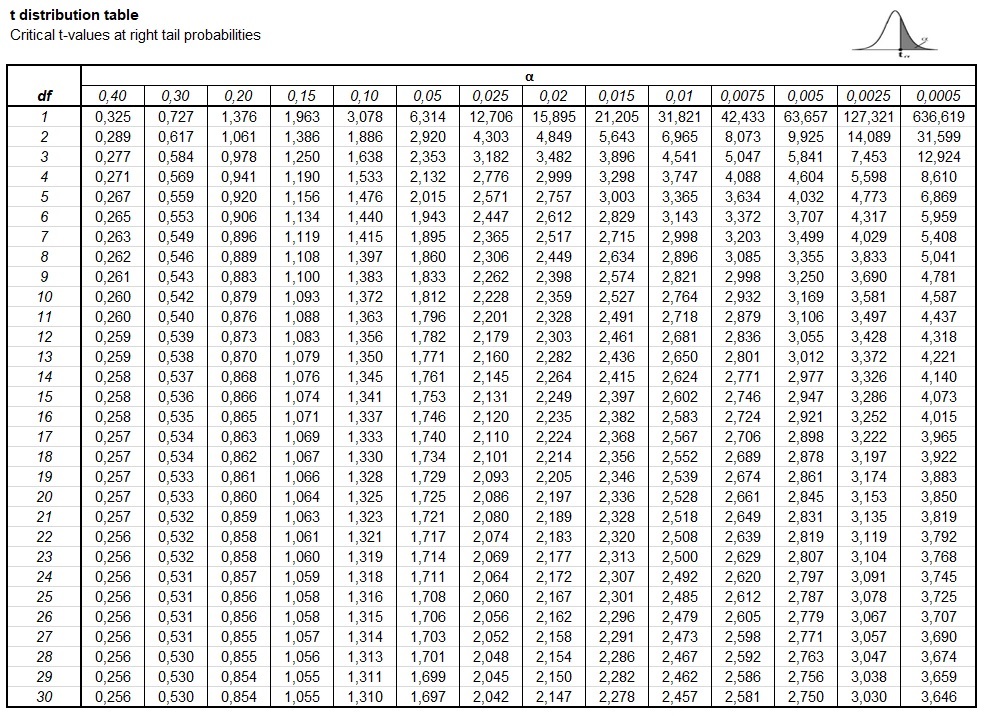
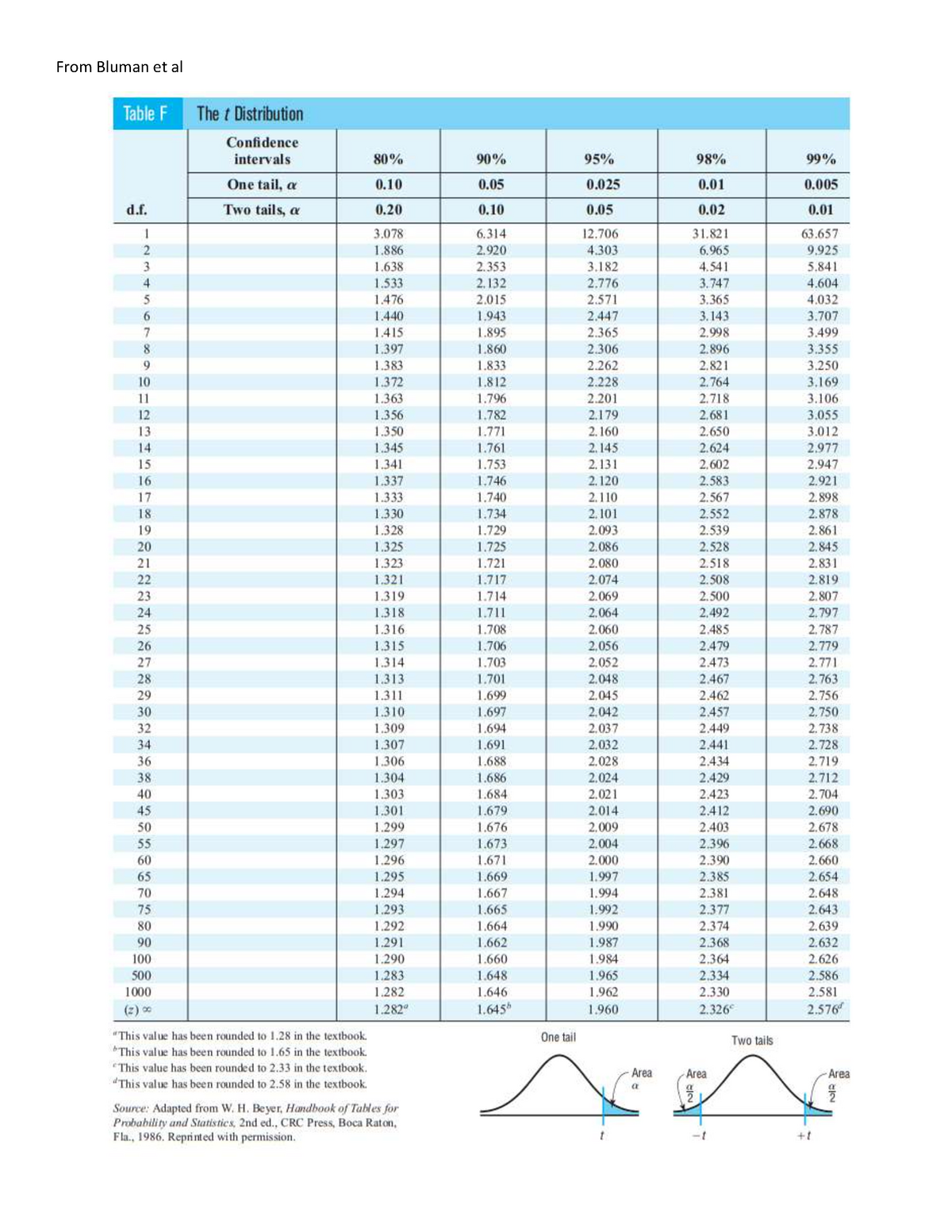
Closure

Thus, we hope this text has supplied helpful insights into Decoding the t-Desk: A Complete Information to Pupil’s t-Distribution. We recognize your consideration to our article. See you in our subsequent article!