Decoding The T-Take a look at Chart: A Complete Information To Crucial Values And Speculation Testing

Decoding the t-Take a look at Chart: A Complete Information to Crucial Values and Speculation Testing

Associated Articles: Decoding the t-Take a look at Chart: A Complete Information to Crucial Values and Speculation Testing

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the t-Take a look at Chart: A Complete Information to Crucial Values and Speculation Testing. Let’s weave fascinating info and provide recent views to the readers.

Decoding the t-Take a look at Chart: A Complete Information to Crucial Values and Speculation Testing

The t-test, a cornerstone of statistical inference, permits researchers to match means between two teams or assess the importance of a single imply towards a hypothesized worth. Central to performing a t-test is using a t-distribution desk, often known as a t-test chart, which supplies vital values vital for figuring out statistical significance. This text delves deep into understanding t-test charts, their interpretation, and their software in varied statistical analyses.

Understanding the t-Distribution

Not like the traditional distribution, the t-distribution is a household of likelihood distributions characterised by its levels of freedom (df). The levels of freedom are associated to the pattern measurement (n) and the variety of teams being in contrast. For a single-sample t-test, df = n – 1. For an impartial samples t-test, df = n1 + n2 – 2, the place n1 and n2 are the pattern sizes of the 2 teams. Because the levels of freedom improve, the t-distribution approaches the traditional distribution.

The t-distribution is bell-shaped and symmetric round zero, however it has heavier tails than the traditional distribution, particularly when the levels of freedom are small. Because of this there is a increased likelihood of observing excessive values within the t-distribution in comparison with the traditional distribution when the pattern measurement is small. This attribute is essential as a result of it accounts for the elevated uncertainty related to smaller samples.

The t-Take a look at Chart: Construction and Interpretation

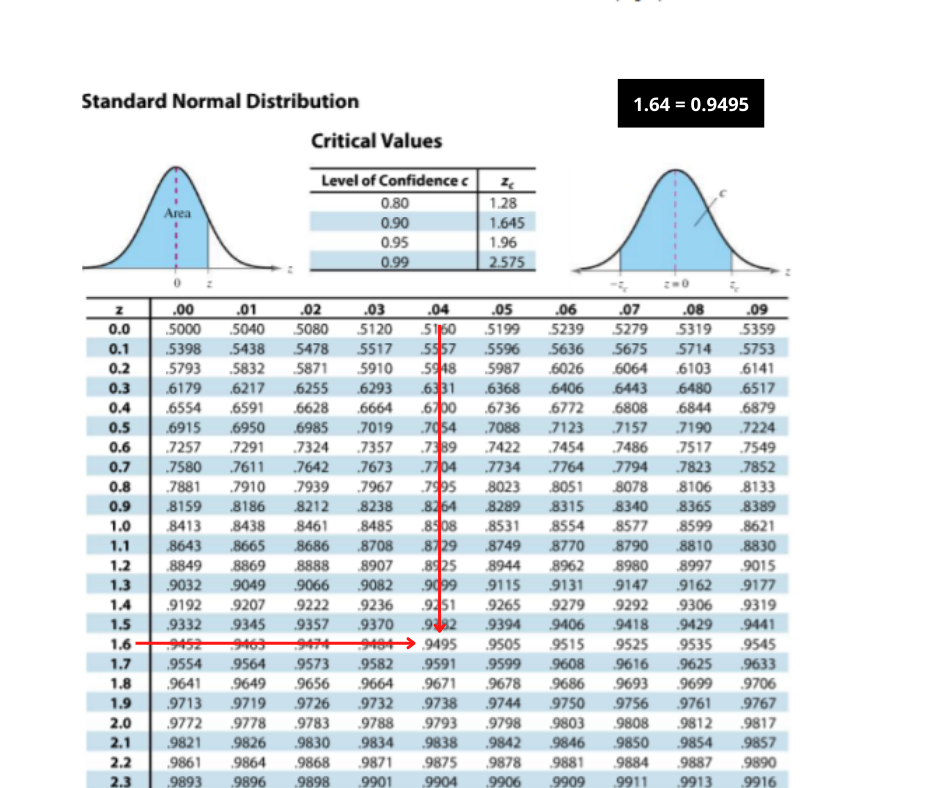
A t-test chart sometimes presents vital values for various ranges of significance (alpha) and levels of freedom. Probably the most generally used alpha ranges are 0.05 (5%) and 0.01 (1%). These alpha ranges symbolize the likelihood of rejecting the null speculation when it’s really true (Kind I error).

The chart is often organized as a desk with rows representing levels of freedom and columns representing alpha ranges (one-tailed and two-tailed exams). Let’s break down the elements:

• Levels of Freedom (df): This means the variety of impartial items of data used to estimate a parameter. As talked about earlier, it is dependent upon the kind of t-test and pattern measurement.

• Significance Stage (α): This represents the likelihood of rejecting the null speculation when it is true. Generally used ranges are 0.05 and 0.01.

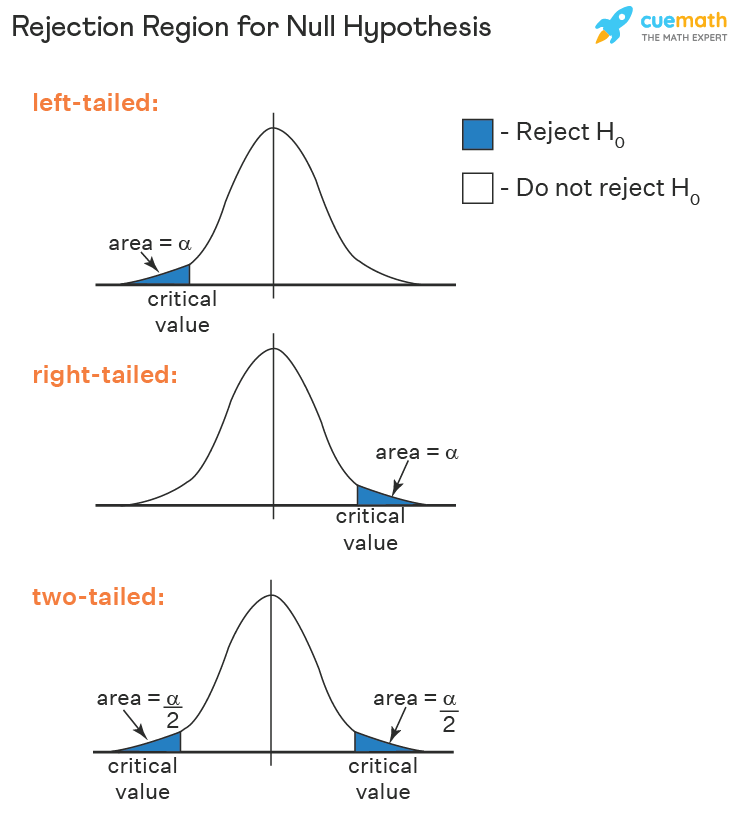
• One-tailed vs. Two-tailed Exams: A one-tailed take a look at examines whether or not the imply of 1 group is considerably better than or lower than the imply of one other group (or a hypothesized worth). A two-tailed take a look at examines whether or not the means are considerably totally different from one another (with out specifying the course of the distinction). The vital values for a one-tailed take a look at are smaller than these for a two-tailed take a look at on the similar alpha degree and levels of freedom.

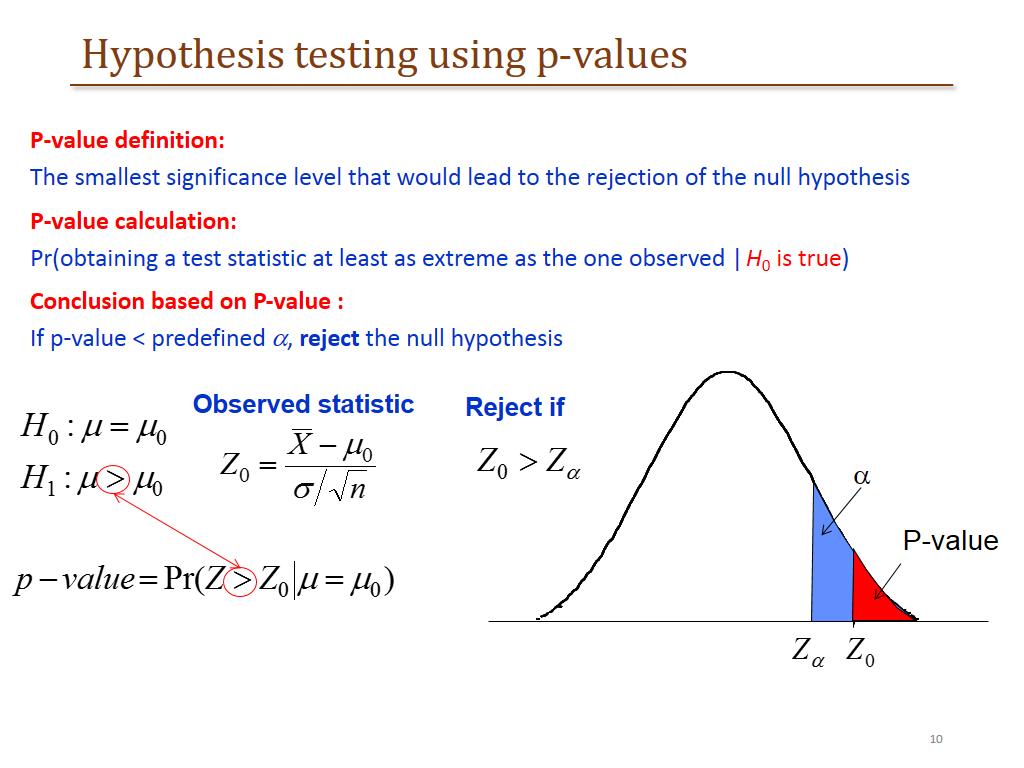
• Crucial Worth (t): That is the worth from the t-distribution that determines whether or not to reject or fail to reject the null speculation. If the calculated t-statistic (obtained from the t-test method) is larger than the vital worth (in absolute worth for a two-tailed take a look at), the null speculation is rejected.

Utilizing the t-Take a look at Chart: A Step-by-Step Information

Let’s illustrate the right way to use a t-test chart with an instance:

Suppose we’re conducting an impartial samples t-test to match the common heights of women and men. We’ve a pattern of 20 males (n1 = 20) and 25 girls (n2 = 25). We calculate a t-statistic of two.15. Our significance degree is 0.05 (α = 0.05), and we’re conducting a two-tailed take a look at.

1. Decide the levels of freedom: df = n1 + n2 – 2 = 20 + 25 – 2 = 43.

2. Determine the importance degree: α = 0.05 (two-tailed).

3. Find the vital worth: Seek the advice of the t-test chart. Discover the row comparable to df = 43. Then, discover the column comparable to α = 0.05 (two-tailed). The intersection of this row and column offers you the vital worth. Let’s assume the vital worth is roughly 2.02.

4. Examine the calculated t-statistic to the vital worth: Our calculated t-statistic (2.15) is larger than the vital worth (2.02).

5. Decide: For the reason that calculated t-statistic exceeds the vital worth, we reject the null speculation. This implies there’s a statistically important distinction within the common heights of women and men on the 0.05 significance degree.

Sorts of t-Exams and Their Corresponding Levels of Freedom

Various kinds of t-tests require totally different calculations for levels of freedom:

• One-sample t-test: Compares the imply of a single pattern to a recognized inhabitants imply. df = n – 1.

• Unbiased samples t-test: Compares the technique of two impartial teams. df = n1 + n2 – 2.

• Paired samples t-test: Compares the technique of two associated teams (e.g., earlier than and after measurements on the identical people). df = n – 1, the place n is the variety of pairs.

Assumptions of the t-Take a look at

The validity of the t-test depends on a number of assumptions:

• Normality: The information ought to be roughly usually distributed, particularly for smaller pattern sizes. Nonetheless, the t-test is comparatively strong to violations of normality, significantly with bigger pattern sizes.

• Independence: Observations ought to be impartial of one another. Because of this the worth of 1 remark doesn’t affect the worth of one other.

• Homogeneity of variances (for impartial samples t-test): The variances of the 2 teams being in contrast ought to be roughly equal. Exams like Levene’s take a look at can be utilized to evaluate this assumption. If the idea is violated, a modified t-test (e.g., Welch’s t-test) can be utilized.

Limitations of the t-Take a look at

Whereas the t-test is a strong software, it has limitations:

• Sensitivity to outliers: Excessive values can considerably affect the outcomes of the t-test.

• Assumption violations: As talked about earlier, violations of normality and homogeneity of variances can have an effect on the validity of the outcomes.

• Restricted to 2 teams: The t-test is primarily designed for evaluating two teams. For evaluating greater than two teams, ANOVA (Evaluation of Variance) is extra acceptable.

Conclusion

The t-test chart is an indispensable software for conducting t-tests and deciphering their outcomes. Understanding the construction of the chart, the that means of levels of freedom and important values, and the assumptions underlying the t-test is essential for conducting legitimate and dependable statistical analyses. By accurately deciphering the t-test chart and contemplating the constraints of the t-test, researchers can draw significant conclusions from their information and make knowledgeable choices primarily based on statistical proof. Keep in mind to at all times contemplate the context of your analysis and select the suitable t-test primarily based in your analysis query and information traits. Moreover, at all times complement your statistical evaluation with a cautious examination of your information and a radical understanding of the subject material.

Closure

Thus, we hope this text has offered precious insights into Decoding the t-Take a look at Chart: A Complete Information to Crucial Values and Speculation Testing. We thanks for taking the time to learn this text. See you in our subsequent article!