Decoding The Two-Tailed T-Statistic Chart: A Complete Information

Decoding the Two-Tailed t-Statistic Chart: A Complete Information

Associated Articles: Decoding the Two-Tailed t-Statistic Chart: A Complete Information

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the Two-Tailed t-Statistic Chart: A Complete Information. Let’s weave attention-grabbing info and supply contemporary views to the readers.

Decoding the Two-Tailed t-Statistic Chart: A Complete Information

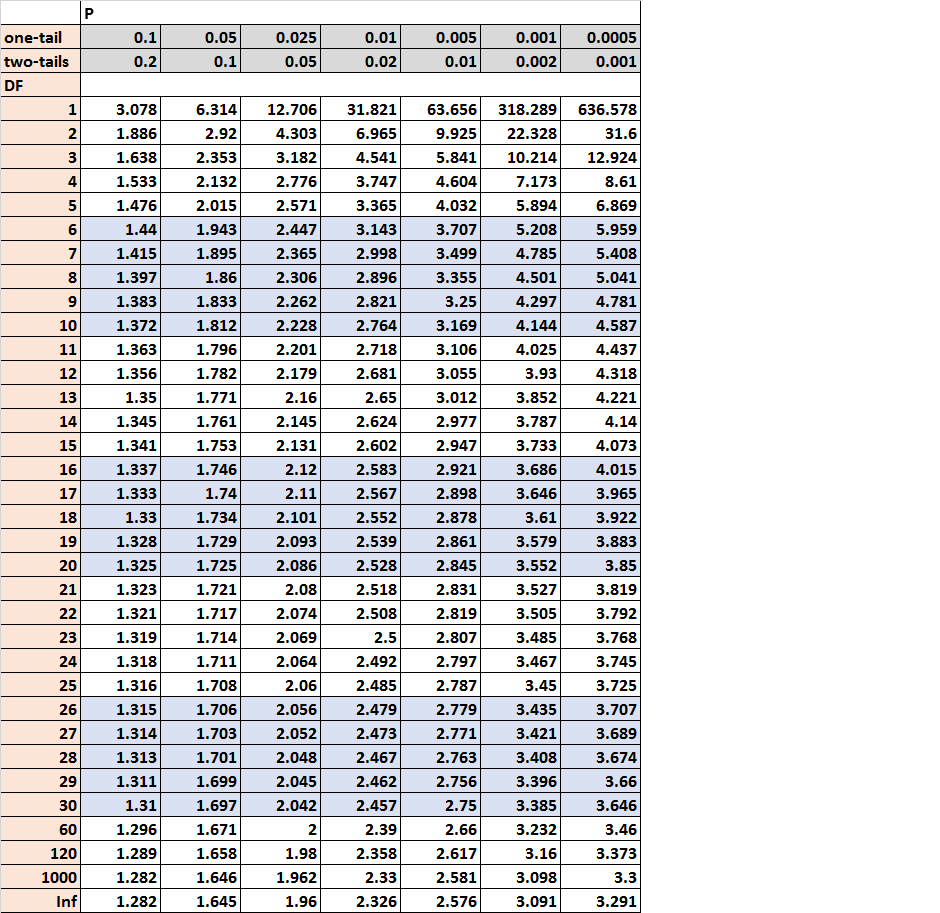
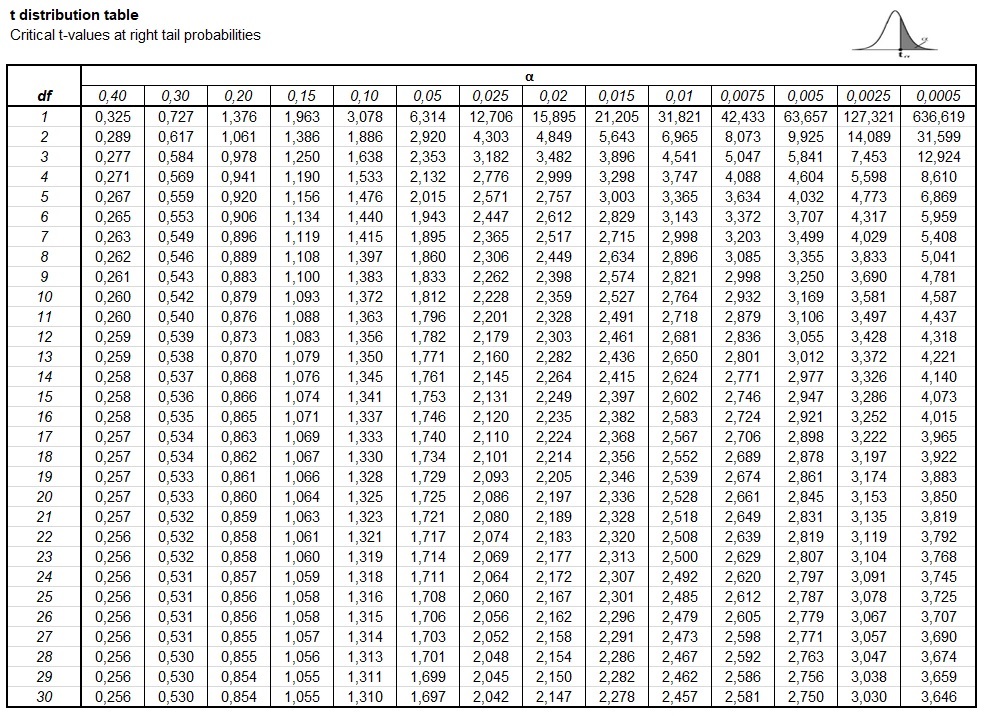
The 2-tailed t-statistic chart, or extra precisely, the t-distribution desk, is an important device in statistical inference. It serves as a lookup desk to find out the crucial t-values wanted for speculation testing, significantly when coping with small pattern sizes the place the traditional distribution might not be an applicable approximation. Understanding this chart is crucial for researchers throughout varied disciplines, from psychology and drugs to engineering and finance. This text offers a complete overview of the two-tailed t-distribution, explaining its development, interpretation, and sensible purposes.

Understanding the t-Distribution:

Not like the usual regular distribution (Z-distribution), which is characterised by a imply of 0 and an ordinary deviation of 1, the t-distribution is a household of distributions. Every member of this household is outlined by its levels of freedom (df). The levels of freedom signify the variety of impartial items of knowledge obtainable to estimate a parameter. In easy phrases, for a pattern of dimension ‘n’, the levels of freedom are usually calculated as ‘n-1’. It is because one diploma of freedom is "misplaced" when estimating the pattern imply, which is used within the calculation of the t-statistic.

The t-distribution is symmetrical and bell-shaped, just like the traditional distribution. Nevertheless, it has heavier tails, which means that it assigns extra chance to excessive values. Because the levels of freedom improve, the t-distribution progressively approaches the traditional distribution. With a sufficiently giant pattern dimension (typically thought of to be n ≥ 30), the distinction between the t-distribution and the traditional distribution turns into negligible.

The Two-Tailed Check:

A two-tailed t-test is used when the researcher is interested by detecting a distinction in both course. For instance, if we’re evaluating the common top of women and men, a two-tailed check could be applicable as a result of we’re interested by figuring out if males are both considerably taller or considerably shorter than ladies. In distinction, a one-tailed check is used when the researcher has a directional speculation, anticipating a distinction in just one particular course.

The 2-tailed t-statistic chart is used to search out the crucial t-values for a given significance stage (α) and levels of freedom (df). The importance stage represents the chance of rejecting the null speculation when it’s truly true (Sort I error). Frequent significance ranges embrace 0.05 (5%) and 0.01 (1%).

Deciphering the t-Distribution Desk:

A typical two-tailed t-distribution desk is organized as follows:

• Rows: Signify the levels of freedom (df).
• Columns: Signify the importance ranges (α), often introduced as α/2 for a two-tailed check. It is because we divide the importance stage equally between the 2 tails of the distribution.
• Cell Values: These are the crucial t-values. If the calculated t-statistic out of your pattern knowledge exceeds the crucial t-value (in absolute worth), you reject the null speculation.

Instance:

As an example we’re conducting a two-tailed t-test with a pattern dimension of 15 (df = 14) and a significance stage of 0.05. To seek out the crucial t-value, we might search for the row comparable to df = 14 and the column comparable to α/2 = 0.025 (0.05/2). The intersection of this row and column will give us the crucial t-value. Let’s assume this worth is 2.145. Which means that if absolutely the worth of our calculated t-statistic is larger than 2.145, we might reject the null speculation on the 0.05 significance stage.

Calculating the t-Statistic:

Earlier than consulting the t-distribution desk, you might want to calculate the t-statistic utilizing the next system:

t = (pattern imply – inhabitants imply) / (pattern normal deviation / √pattern dimension)

The place:

• Pattern imply is the common of your pattern knowledge.
• Inhabitants imply is the hypothesized imply below the null speculation.
• Pattern normal deviation is a measure of the variability in your pattern knowledge.
• Pattern dimension is the variety of observations in your pattern.

Functions of the Two-Tailed t-Check:

The 2-tailed t-test has a variety of purposes in varied fields:

• Evaluating Means: Testing whether or not there’s a vital distinction between the technique of two impartial teams (e.g., evaluating the common check scores of two totally different instructing strategies). This entails utilizing the impartial samples t-test.
• Paired Samples t-test: Evaluating the technique of two associated teams (e.g., evaluating the blood stress of sufferers earlier than and after taking a drugs). This entails utilizing the paired samples t-test.
• One-Pattern t-test: Evaluating the imply of a single pattern to a identified inhabitants imply (e.g., testing whether or not the common weight of a specific kind of fruit is totally different from a acknowledged worth).

Limitations of the t-Distribution:

Whereas the t-distribution is a robust device, it has sure limitations:

• Assumption of Normality: The t-test assumes that the information is generally distributed. Whereas the t-test is comparatively strong to violations of this assumption, particularly with bigger pattern sizes, vital deviations from normality can have an effect on the validity of the outcomes. Non-parametric options must be thought of if the normality assumption is severely violated.
• Homogeneity of Variance (for Impartial Samples t-test): The impartial samples t-test assumes that the variances of the 2 teams being in contrast are equal. If this assumption is violated, a modified model of the t-test, similar to Welch’s t-test, must be used.
• Small Pattern Sizes: Whereas the t-distribution is designed for small pattern sizes, extraordinarily small pattern sizes (e.g., n < 5) can nonetheless result in unreliable outcomes.

Software program and On-line Calculators:

Many statistical software program packages (e.g., SPSS, R, SAS, STATA) and on-line calculators can carry out t-tests and supply p-values instantly, eliminating the necessity for guide lookup within the t-distribution desk. Nevertheless, understanding the underlying rules and the interpretation of the t-distribution desk stays essential for comprehending the outcomes and making knowledgeable selections.

Conclusion:

The 2-tailed t-distribution desk is a basic device in statistical evaluation, enabling researchers to make inferences about inhabitants parameters primarily based on pattern knowledge. Understanding its development, interpretation, and limitations is crucial for accurately making use of the t-test and drawing legitimate conclusions from the outcomes. Whereas software program packages simplify the method, a grasp of the underlying rules ensures a deeper understanding of statistical inference and the reliability of the findings. Keep in mind to at all times contemplate the assumptions of the t-test and select applicable various strategies if essential. By mastering using the t-distribution desk, researchers can confidently analyze their knowledge and contribute to the development of data of their respective fields.

Closure

Thus, we hope this text has supplied invaluable insights into Decoding the Two-Tailed t-Statistic Chart: A Complete Information. We admire your consideration to our article. See you in our subsequent article!