Decoding The Z-Desk: A Complete Information With Examples

Decoding the Z-Desk: A Complete Information with Examples

Associated Articles: Decoding the Z-Desk: A Complete Information with Examples

Introduction

On this auspicious event, we’re delighted to delve into the intriguing matter associated to Decoding the Z-Desk: A Complete Information with Examples. Let’s weave attention-grabbing info and supply contemporary views to the readers.

Decoding the Z-Desk: A Complete Information with Examples

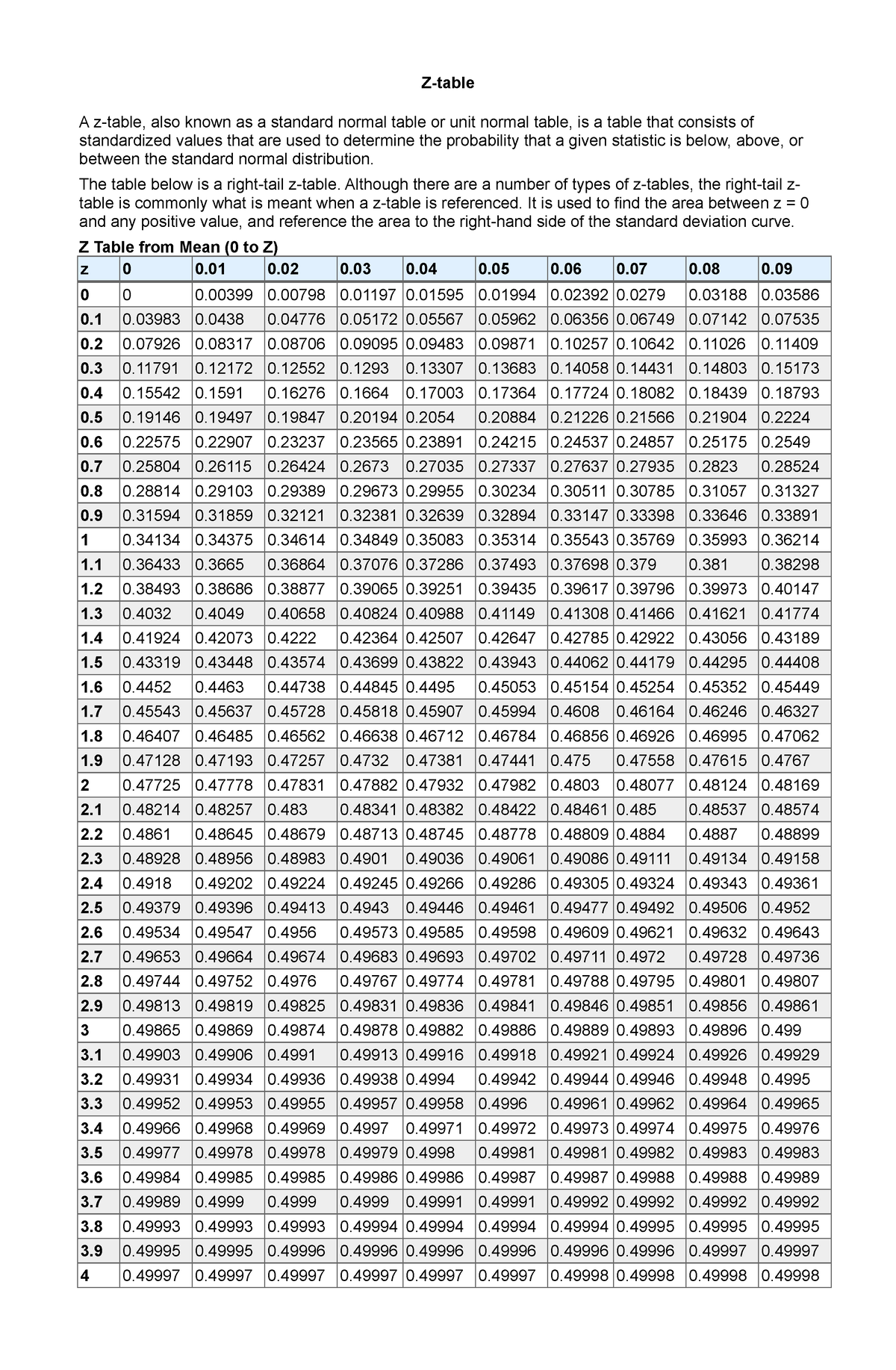
The Z-table, also referred to as the usual regular distribution desk, is a vital software in statistics. It gives the chances related to completely different values of the usual regular distribution, a bell-shaped curve with a imply of 0 and an ordinary deviation of 1. Understanding and using the Z-table is prime for varied statistical analyses, from speculation testing to confidence interval calculations. This text will present a radical rationalization of the Z-table, its building, the right way to interpret it, and illustrate its utility with sensible examples. We’ll discover each the constructive and adverse Z-scores and delve into the nuances of discovering possibilities for particular ranges.

Understanding the Commonplace Regular Distribution

Earlier than diving into the Z-table itself, it is essential to grasp the usual regular distribution. This distribution is a theoretical chance distribution with the next traits:

• Imply (μ) = 0: The typical worth of the distribution is zero.
• Commonplace Deviation (σ) = 1: The unfold or dispersion of the info is one unit.
• Symmetrical: The distribution is completely symmetrical round its imply. The realm below the curve to the left of the imply is the same as the world below the curve to the correct of the imply (each are 0.5).
• Steady: The distribution is steady, which means that any worth throughout the vary is feasible.

The Z-score, typically referred to as an ordinary rating, represents the variety of normal deviations a selected information level is away from the imply of the distribution. A constructive Z-score signifies the info level is above the imply, whereas a adverse Z-score signifies it is beneath the imply. The components for calculating a Z-score is:

Z = (X – μ) / σ

The place:

• Z is the Z-score
• X is the info level
• μ is the inhabitants imply
• σ is the inhabitants normal deviation

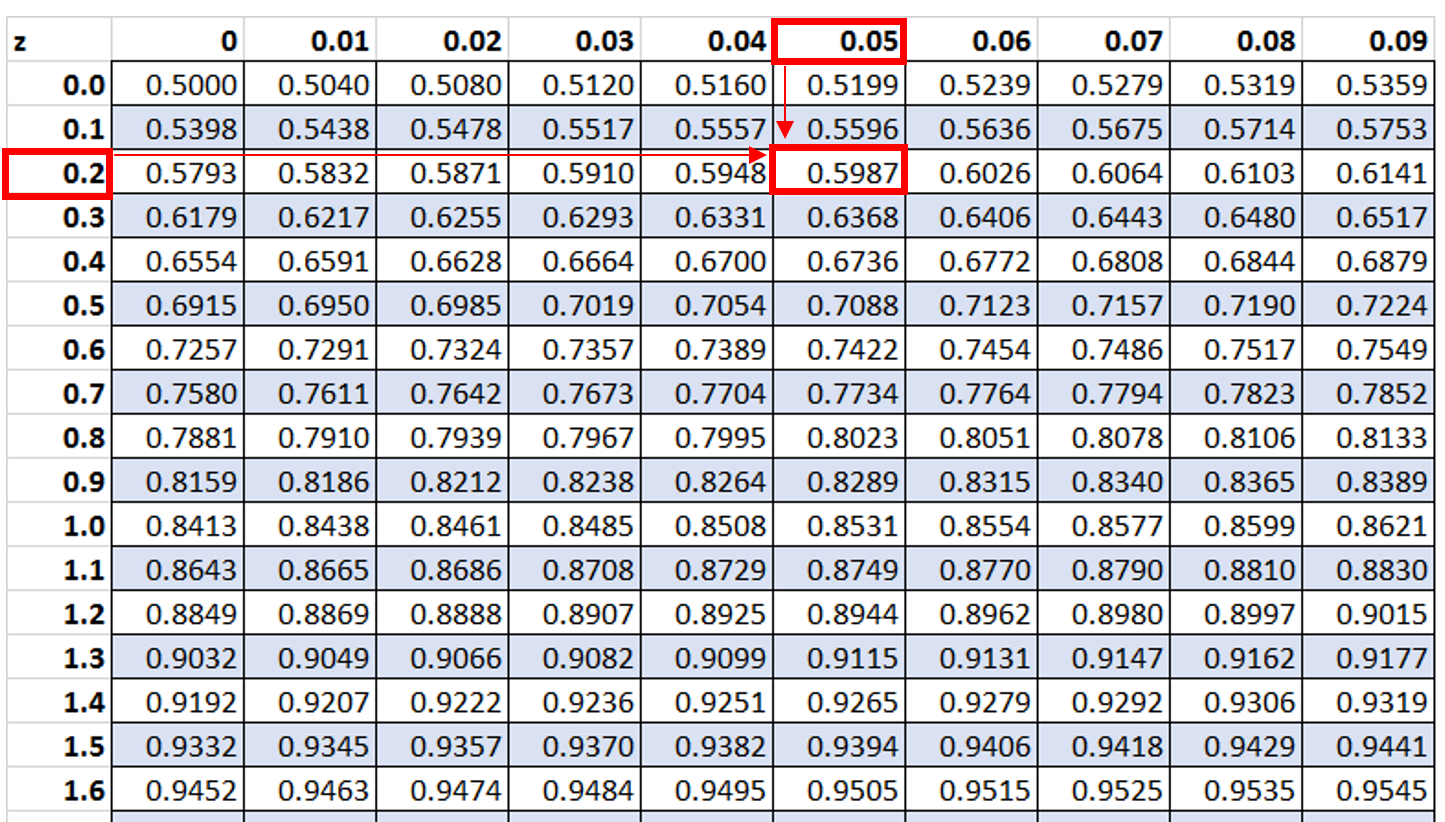
Construction and Interpretation of the Z-Desk

The Z-table is organized to offer the cumulative chance (space below the curve) to the left of a given Z-score. It is usually offered as a two-dimensional desk. The rows signify the entire quantity and the primary decimal place of the Z-score, whereas the columns signify the second decimal place.

For instance, to seek out the chance related to a Z-score of 1.96, you’ll:

1. Find the row comparable to 1.9.
2. Find the column comparable to 0.06.
3. The worth on the intersection of the row and column is the cumulative chance. On this case, it is roughly 0.9750. This implies that there’s a 97.5% chance {that a} randomly chosen information level from the usual regular distribution might be lower than or equal to 1.96.

Utilizing the Z-Desk: Examples

Let’s illustrate the utilization of the Z-table with a number of examples:

Instance 1: Discovering the chance for a constructive Z-score

Discover the chance {that a} randomly chosen information level from an ordinary regular distribution is lower than 1.52.

1. Find the row comparable to 1.5.
2. Find the column comparable to 0.02.
3. The intersection worth is roughly 0.9357. Due to this fact, P(Z < 1.52) ≈ 0.9357.

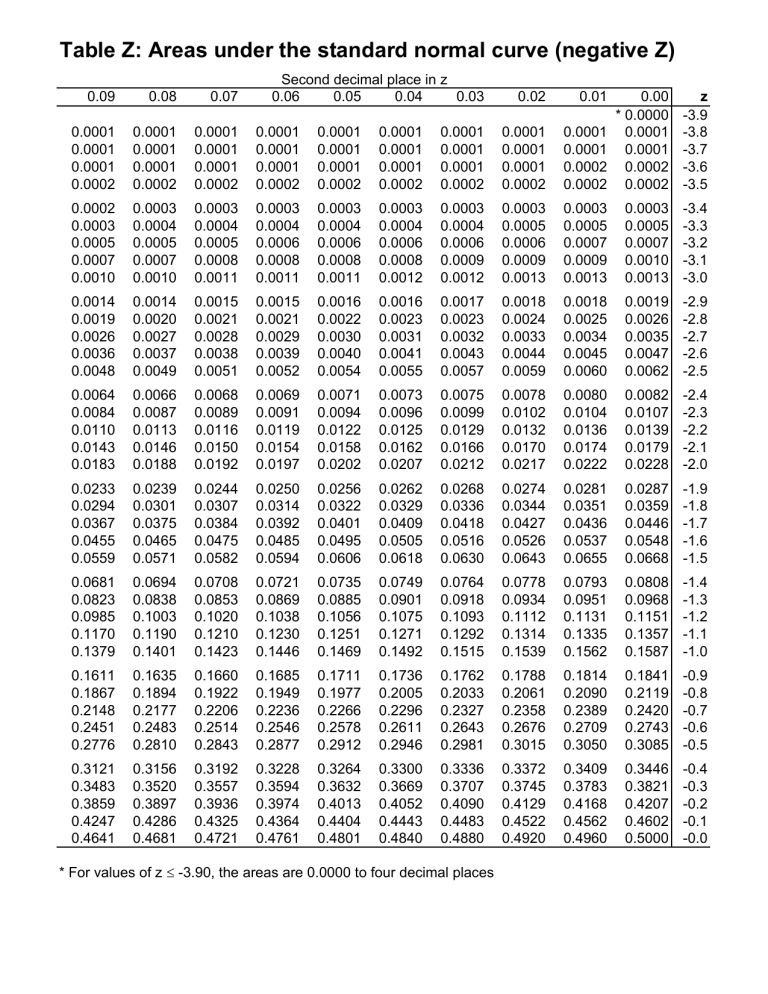
Instance 2: Discovering the chance for a adverse Z-score

Discover the chance {that a} randomly chosen information level is lower than -0.85.

1. Find the row comparable to -0.8.
2. Find the column comparable to 0.05.
3. The intersection worth is roughly 0.1977. Due to this fact, P(Z < -0.85) ≈ 0.1977. Do not forget that resulting from symmetry, P(Z < -0.85) = P(Z > 0.85) = 1 – P(Z < 0.85).

Instance 3: Discovering the chance between two Z-scores

Discover the chance {that a} randomly chosen information level lies between Z = -1.0 and Z = 1.0.

1. Discover P(Z < 1.0) ≈ 0.8413.
2. Discover P(Z < -1.0) ≈ 0.1587.
3. Subtract the smaller chance from the bigger chance: 0.8413 – 0.1587 = 0.6826. Due to this fact, P(-1.0 < Z < 1.0) ≈ 0.6826. This represents roughly 68% of the info falling inside one normal deviation of the imply.

Instance 4: Discovering the Z-score for a given chance

Discover the Z-score such that the chance of an information level being lower than that Z-score is 0.90.

1. Search for the closest worth to 0.90 within the physique of the Z-table.
2. The closest worth is roughly 0.8997, which corresponds to a Z-score of 1.28. Due to this fact, P(Z < 1.28) ≈ 0.90.

Limitations and Concerns

Whereas the Z-table is a robust software, it has limitations:

• Approximation: The values within the Z-table are approximations. Extra exact values will be obtained utilizing statistical software program or calculators.
• Commonplace Regular Distribution: The Z-table is particularly designed for the usual regular distribution. To make use of it with different regular distributions, it’s essential to first standardize the info utilizing the Z-score components.
• Interpolation: For Z-scores circuitously listed within the desk, interpolation can be utilized to estimate the chance. Nonetheless, this introduces additional approximation.

Functions of the Z-Desk

The Z-table finds purposes in varied statistical contexts:

• Speculation testing: Figuring out the p-value for a Z-test.
• Confidence intervals: Calculating confidence intervals for inhabitants means and proportions.
• Course of functionality evaluation: Assessing the aptitude of a course of to fulfill specs.
• High quality management: Monitoring and bettering the standard of services or products.
• Likelihood calculations: Figuring out the chance of occasions associated to usually distributed variables.

Conclusion

The Z-table is an indispensable software for anybody working with statistical information. Mastering its use is essential for understanding and decoding statistical outcomes precisely. By understanding the usual regular distribution, the construction of the Z-table, and the examples offered, you’ll be able to confidently apply this software to resolve a variety of statistical issues. Bear in mind to all the time think about the constraints of the Z-table and make the most of extra exact strategies when essential, particularly when excessive accuracy is required. With follow and cautious consideration to element, the Z-table will grow to be a useful asset in your statistical toolkit.

Closure

Thus, we hope this text has offered helpful insights into Decoding the Z-Desk: A Complete Information with Examples. We respect your consideration to our article. See you in our subsequent article!