Decoding The Z-Worth Chart: A Complete Information To Understanding And Making use of The Customary Regular Distribution

Decoding the Z-Worth Chart: A Complete Information to Understanding and Making use of the Customary Regular Distribution

Associated Articles: Decoding the Z-Worth Chart: A Complete Information to Understanding and Making use of the Customary Regular Distribution

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the Z-Worth Chart: A Complete Information to Understanding and Making use of the Customary Regular Distribution. Let’s weave fascinating info and provide recent views to the readers.

Decoding the Z-Worth Chart: A Complete Information to Understanding and Making use of the Customary Regular Distribution

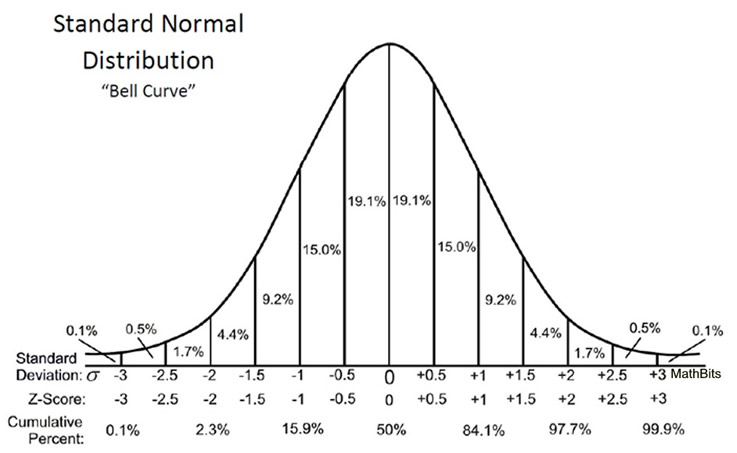
The Z-value chart, also called the usual regular distribution desk, is a basic software in statistics. It is a cornerstone for speculation testing, confidence interval calculation, and understanding chances related to usually distributed knowledge. This complete information will delve into the intricacies of the Z-value chart, explaining its development, interpretation, and sensible functions with illustrative examples.

Understanding the Customary Regular Distribution:

Earlier than diving into the Z-value chart itself, it is essential to understand the idea of the usual regular distribution. It is a particular sort of regular distribution with a imply (µ) of 0 and an ordinary deviation (σ) of 1. The conventional distribution, typically visualized as a bell curve, is a steady likelihood distribution that describes many naturally occurring phenomena. Its symmetrical form implies that knowledge factors are clustered across the imply, with progressively fewer knowledge factors additional away from the imply.

The usual regular distribution simplifies calculations and comparisons throughout completely different regular distributions. Any usually distributed variable might be reworked into an ordinary regular variable (Z-score) utilizing a easy method:

Z = (X – µ) / σ

The place:

• Z is the Z-score (customary rating)
• X is the uncooked rating from the unique regular distribution
• µ is the imply of the unique regular distribution
• σ is the usual deviation of the unique distribution

This transformation permits us to make use of a single desk (the Z-value chart) to find out chances for any usually distributed variable, no matter its authentic imply and customary deviation.

The Construction and Interpretation of the Z-Worth Chart:

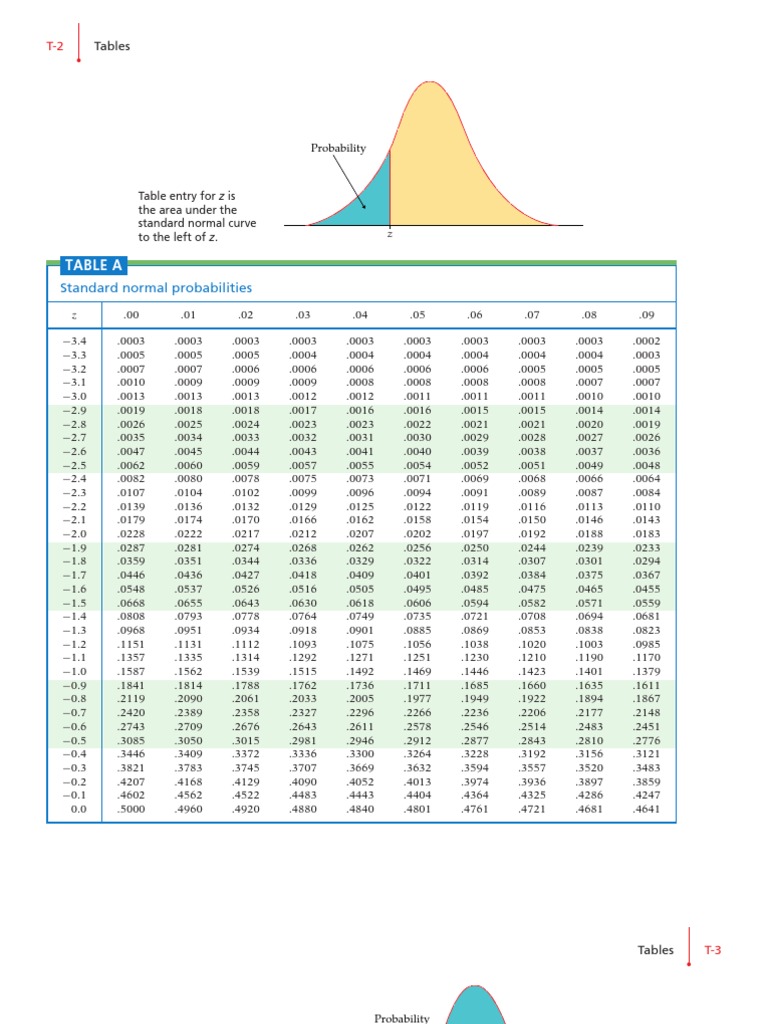
The Z-value chart presents chances related to Z-scores. Sometimes, it is organized in a tabular format, with Z-scores listed alongside the rows and columns. The rows normally symbolize the entire quantity and tenths place of the Z-score, whereas the columns symbolize the hundredths place. The intersection of a row and column provides the cumulative likelihood (space beneath the curve) to the left of that particular Z-score.

For instance, when you search for a Z-score of 1.96, you will discover a likelihood of roughly 0.975. Which means there is a 97.5% likelihood {that a} randomly chosen knowledge level from an ordinary regular distribution will fall beneath 1.96 customary deviations from the imply. Conversely, there is a 2.5% likelihood it’s going to fall above 1.96 customary deviations. Because of the symmetry of the distribution, the realm to the best of a Z-score is just 1 minus the realm to the left.

Utilizing the Z-Worth Chart for Chance Calculations:

The Z-value chart is extremely versatile for varied likelihood calculations:

• Discovering the likelihood of a rating falling inside a particular vary: To search out the likelihood of a rating falling between two Z-scores (e.g., between Z1 and Z2), you discover the cumulative likelihood for Z2 and subtract the cumulative likelihood for Z1.

• Discovering the Z-score similar to a particular likelihood: If you recognize the likelihood and need to discover the corresponding Z-score, you merely search for the likelihood within the physique of the desk and discover the related Z-score.

• Figuring out percentiles: Percentiles symbolize the worth beneath which a sure proportion of knowledge falls. For instance, the ninety fifth percentile corresponds to the Z-score that has a cumulative likelihood of 0.95.

• Speculation testing: The Z-value chart performs a important position in speculation testing, the place you examine a calculated Z-statistic to important Z-values (obtained from the chart) to find out whether or not to reject or fail to reject a null speculation.

Examples of Z-Worth Chart Functions:

Let’s illustrate the functions with some examples:

Instance 1: Discovering the likelihood of a rating falling beneath a sure worth.

Suppose the common peak of grownup ladies in a inhabitants is 165 cm with an ordinary deviation of 5 cm. What’s the likelihood {that a} randomly chosen lady is shorter than 170 cm?

1. Calculate the Z-score: Z = (170 – 165) / 5 = 1
2. Seek the advice of the Z-value chart: Search for Z = 1.00. The likelihood is roughly 0.8413.
3. Interpretation: There may be an 84.13% likelihood {that a} randomly chosen lady is shorter than 170 cm.

Instance 2: Discovering the likelihood of a rating falling inside a spread.

Utilizing the identical peak knowledge, what’s the likelihood {that a} randomly chosen lady’s peak is between 160 cm and 170 cm?

1. Calculate Z-scores: Z1 = (160 – 165) / 5 = -1; Z2 = (170 – 165) / 5 = 1
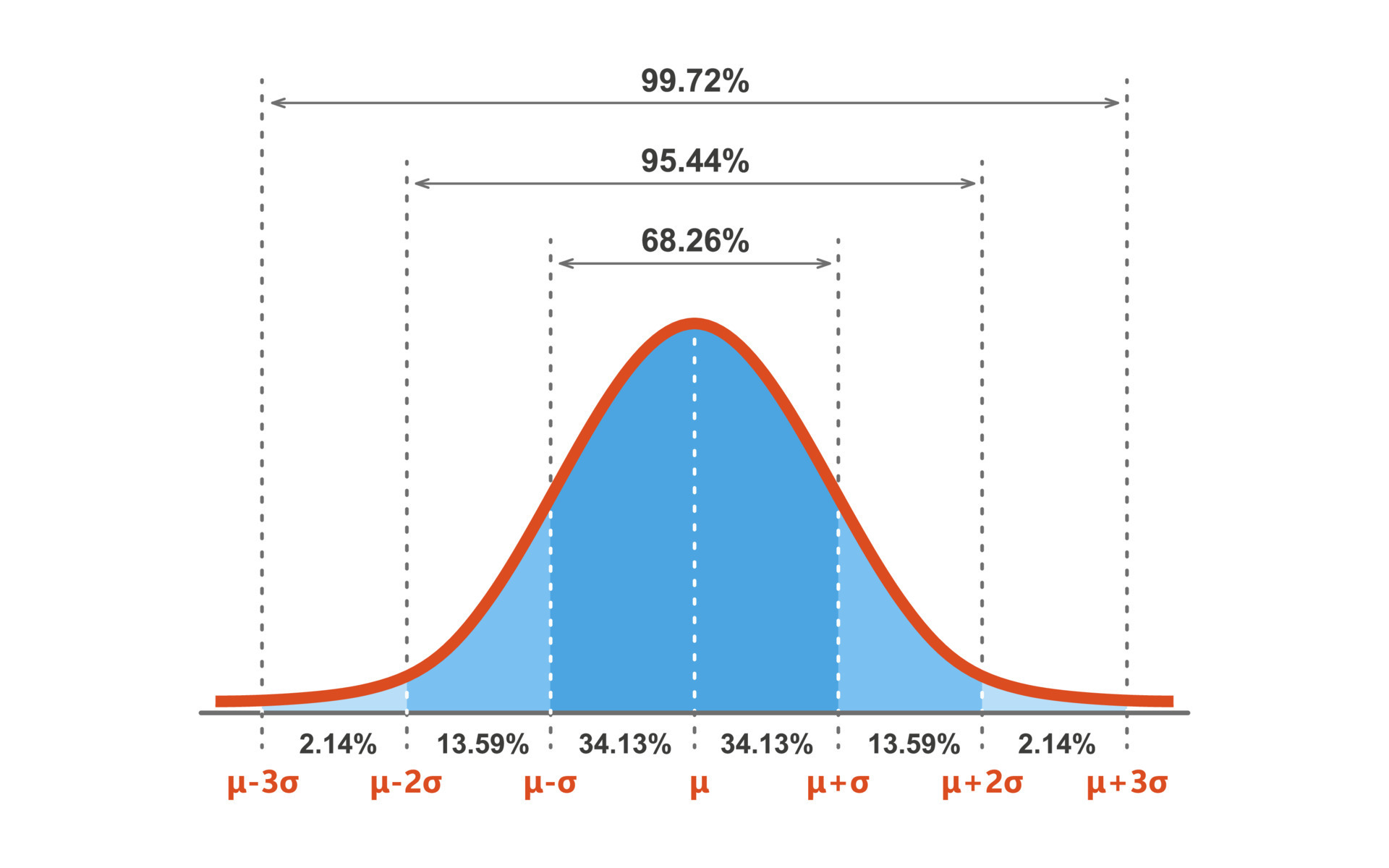
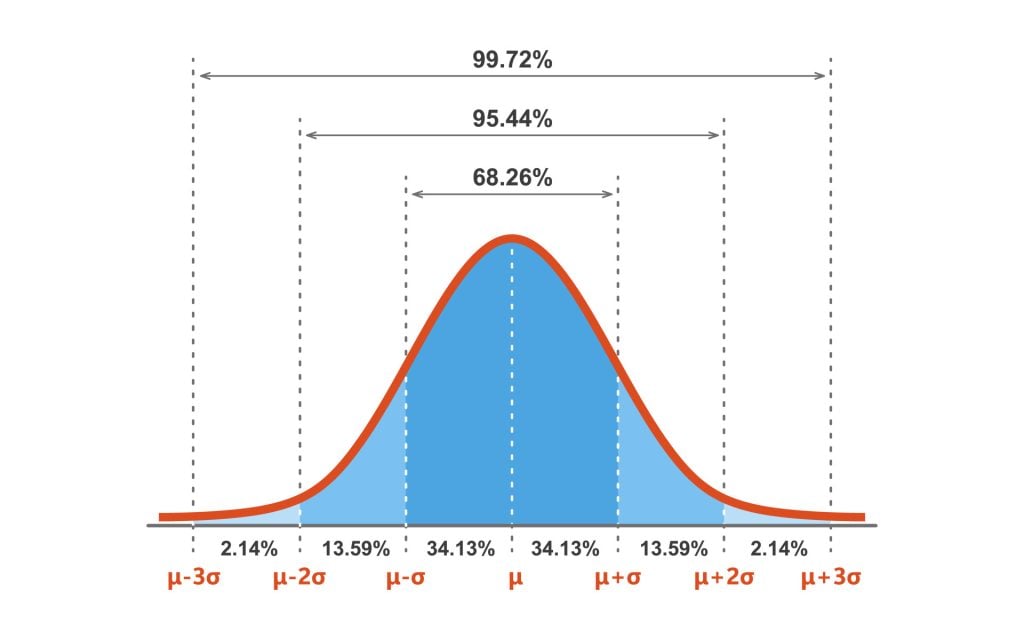
2. Seek the advice of the Z-value chart: The likelihood for Z1 = -1 is roughly 0.1587, and for Z2 = 1 is roughly 0.8413.
3. Calculate the distinction: 0.8413 – 0.1587 = 0.6826
4. Interpretation: There’s a 68.26% likelihood {that a} randomly chosen lady’s peak is between 160 cm and 170 cm.

Instance 3: Discovering a Z-score for a given percentile.

What’s the Z-score that corresponds to the ninetieth percentile?

1. Search for the likelihood: Discover the likelihood closest to 0.90 within the Z-value chart.
2. Establish the Z-score: The corresponding Z-score is roughly 1.28.
3. Interpretation: A Z-score of 1.28 represents the ninetieth percentile of the usual regular distribution.

Limitations and Concerns:

Whereas the Z-value chart is a strong software, it is important to concentrate on its limitations:

• Assumes normality: The Z-value chart is just relevant to knowledge that follows a traditional distribution. If the info is considerably skewed or non-normal, utilizing the Z-value chart can result in inaccurate outcomes. Assessments for normality, just like the Shapiro-Wilk take a look at, ought to be carried out earlier than making use of Z-tests.

• Accuracy: The Z-value chart gives approximate chances. Extra exact calculations might be obtained utilizing statistical software program or calculators.

• Coping with giant datasets: For very giant datasets, the central restrict theorem can be utilized to approximate the sampling distribution, even when the underlying inhabitants is not completely regular.

Conclusion:

The Z-value chart is an indispensable software for anybody working with statistical knowledge. Understanding its development, interpretation, and functions is essential for conducting correct statistical analyses, making knowledgeable selections, and drawing significant conclusions from knowledge. Whereas its limitations ought to be acknowledged, the Z-value chart stays a cornerstone of statistical inference and a invaluable asset in varied fields, from drugs and engineering to finance and social sciences. By mastering its use, one features a strong software for unraveling the complexities of knowledge and extracting invaluable insights.

Closure

Thus, we hope this text has offered invaluable insights into Decoding the Z-Worth Chart: A Complete Information to Understanding and Making use of the Customary Regular Distribution. We hope you discover this text informative and helpful. See you in our subsequent article!