The Indispensable Integration Method Chart: A Complete Information

The Indispensable Integration Method Chart: A Complete Information

Associated Articles: The Indispensable Integration Method Chart: A Complete Information

Introduction

With enthusiasm, let’s navigate by way of the intriguing subject associated to The Indispensable Integration Method Chart: A Complete Information. Let’s weave fascinating data and provide contemporary views to the readers.

The Indispensable Integration Method Chart: A Complete Information

Integration, the reverse strategy of differentiation, is a cornerstone of calculus with far-reaching purposes in numerous fields like physics, engineering, economics, and statistics. Mastering integration requires a strong understanding of basic integration formulation and strategies. This text serves as a complete information to important integration formulation, categorized for readability and accompanied by explanations and examples to facilitate understanding and utility.

I. Primary Integration Formulation: The Constructing Blocks

These formulation symbolize the foundational parts upon which extra advanced integration strategies are constructed. Memorizing these is essential for environment friendly problem-solving.

1. Energy Rule: ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, the place n ≠ -1. That is probably the most basic rule, relevant to integrating powers of x. The fixed of integration, C, accounts for the infinite variety of antiderivatives a perform can possess.

   • Instance: ∫x³ dx = (x⁴)/4 + C

2. Fixed A number of Rule: ∫ok f(x) dx = ok ∫f(x) dx, the place ok is a continuing. This enables us to tug fixed components out of the integral.

   • Instance: ∫5x² dx = 5 ∫x² dx = 5(x³/3) + C = (5x³)/3 + C

3. Sum/Distinction Rule: ∫[f(x) ± g(x)] dx = ∫f(x) dx ± ∫g(x) dx. This rule permits us to combine sums and variations of features time period by time period.

   • Instance: ∫(x² + 2x – 1) dx = ∫x² dx + ∫2x dx – ∫1 dx = (x³/3) + x² – x + C

4. Integrals of Trigonometric Capabilities:

   • ∫sin(x) dx = -cos(x) + C
   • ∫cos(x) dx = sin(x) + C
   • ∫tan(x) dx = ln|sec(x)| + C
   • ∫cot(x) dx = ln|sin(x)| + C
   • ∫sec(x) dx = ln|sec(x) + tan(x)| + C
   • ∫csc(x) dx = ln|csc(x) – cot(x)| + C
   • ∫sec²(x) dx = tan(x) + C
   • ∫csc²(x) dx = -cot(x) + C
   • ∫sec(x)tan(x) dx = sec(x) + C
   • ∫csc(x)cot(x) dx = -csc(x) + C

5. Integrals of Exponential and Logarithmic Capabilities:

   • ∫eˣ dx = eˣ + C
   • ∫aˣ dx = (aˣ)/ln(a) + C, the place a > 0 and a ≠ 1
   • ∫(1/x) dx = ln|x| + C

II. Superior Integration Methods: Increasing the Arsenal

Whereas the fundamental formulation cowl many conditions, extra advanced integrals require superior strategies.

1. Integration by Substitution (u-Substitution): This system entails substituting a portion of the integrand with a brand new variable, ‘u’, to simplify the integral. The secret’s selecting an acceptable ‘u’ such that its spinoff can be current (or simply manipulated to be current) within the integrand.

   • Instance: ∫x(x² + 1)³ dx. Let u = x² + 1, then du = 2x dx. The integral turns into (1/2)∫u³ du = (1/2)(u⁴)/4 + C = (x² + 1)⁴/8 + C.

2. Integration by Elements: This system is predicated on the product rule of differentiation and is especially helpful for integrating merchandise of features. The system is: ∫u dv = uv – ∫v du. The selection of ‘u’ and ‘dv’ is essential and infrequently entails the LIATE rule (Logarithmic, Inverse Trigonometric, Algebraic, Trigonometric, Exponential) to prioritize the selection of ‘u’.

   • Instance: ∫x cos(x) dx. Let u = x and dv = cos(x) dx. Then du = dx and v = sin(x). The integral turns into x sin(x) – ∫sin(x) dx = x sin(x) + cos(x) + C.

3. Partial Fraction Decomposition: This system is used to combine rational features (fractions of polynomials). It entails decomposing the rational perform into less complicated fractions that may be built-in individually.

   • Instance: ∫(2x + 1)/(x² + x) dx. The denominator components as x(x+1). Partial fraction decomposition yields A/x + B/(x+1). Fixing for A and B offers A=1 and B=1. The integral turns into ∫(1/x + 1/(x+1)) dx = ln|x| + ln|x+1| + C = ln|x(x+1)| + C.

4. Trigonometric Substitution: This system is used to combine expressions containing sq. roots of quadratic expressions. Particular trigonometric substitutions are employed to simplify the integrand.

   • Instance: ∫√(1 – x²) dx. Let x = sin(θ), then dx = cos(θ) dθ. The integral turns into ∫cos²(θ) dθ, which will be solved utilizing trigonometric identities.

5. Desk of Integrals: In depth tables of integrals exist, offering options to a variety of integrals. These tables are invaluable assets for each college students and professionals. Nonetheless, understanding the underlying strategies stays essential for efficient problem-solving and for dealing with integrals not present in commonplace tables.

III. Particular Integrals and Purposes

Particular integrals prolong the idea of integration by incorporating limits of integration, leading to a numerical worth fairly than a household of features. The Elementary Theorem of Calculus connects particular and indefinite integrals:

∫[a,b] f(x) dx = F(b) – F(a), the place F(x) is an antiderivative of f(x).

Particular integrals discover intensive purposes in numerous fields:

• Space Calculation: The world below a curve between two factors will be calculated utilizing particular integration.
• Quantity Calculation: Volumes of solids of revolution will be decided utilizing integration strategies just like the disk or shell methodology.
• Work Calculation: The work performed by a pressure will be calculated utilizing integration.
• Likelihood and Statistics: Likelihood distributions and statistical moments are sometimes outlined utilizing integrals.
• Physics: Integration is used extensively in mechanics, electromagnetism, and fluid dynamics to resolve issues involving movement, forces, and fields.

IV. Past the Chart: Numerical Integration

When analytical options are unavailable or impractical, numerical integration strategies present approximate options. Strategies just like the trapezoidal rule, Simpson’s rule, and Gaussian quadrature provide methods to estimate particular integrals utilizing numerical approximations.

V. Conclusion

This text gives a complete overview of integration formulation and strategies. Whereas a system chart serves as a invaluable reference, a deep understanding of the underlying ideas and the power to decide on the suitable method for a given downside are important for mastering integration. Apply is vital to creating proficiency, and tackling a various vary of issues is essential for solidifying understanding and constructing confidence in making use of these basic instruments of calculus. Keep in mind to all the time test your options and perceive the context of the issue to make sure the accuracy and relevance of your outcomes. The journey of mastering integration is a steady strategy of studying and refinement, rewarding those that persevere with a robust and versatile software for fixing advanced issues.

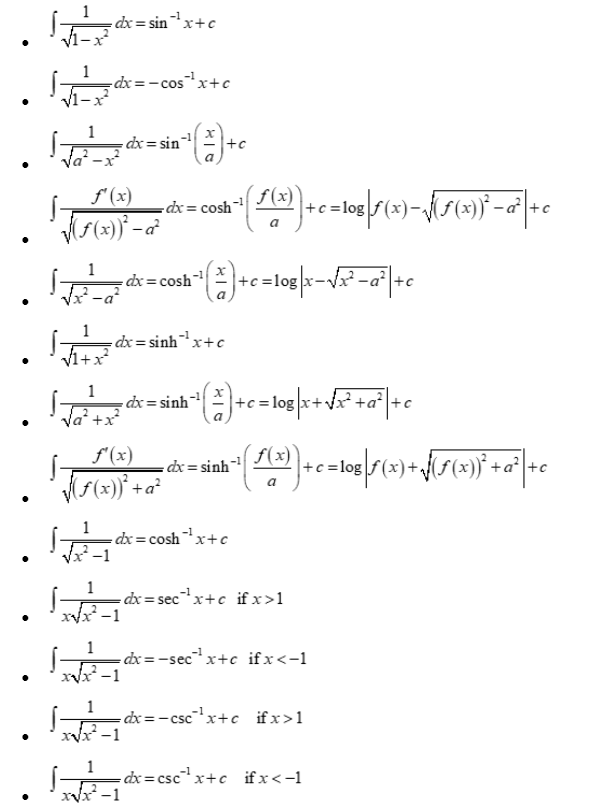
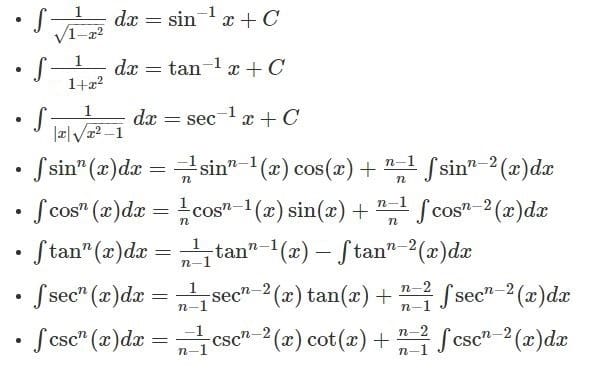
Closure

Thus, we hope this text has supplied invaluable insights into The Indispensable Integration Method Chart: A Complete Information. We hope you discover this text informative and helpful. See you in our subsequent article!