Understanding and Making use of the p-Chart Management Limits System: A Complete Information
Associated Articles: Understanding and Making use of the p-Chart Management Limits System: A Complete Information
Introduction
With nice pleasure, we’ll discover the intriguing subject associated to Understanding and Making use of the p-Chart Management Limits System: A Complete Information. Let’s weave fascinating data and provide contemporary views to the readers.
Desk of Content material
Understanding and Making use of the p-Chart Management Limits System: A Complete Information
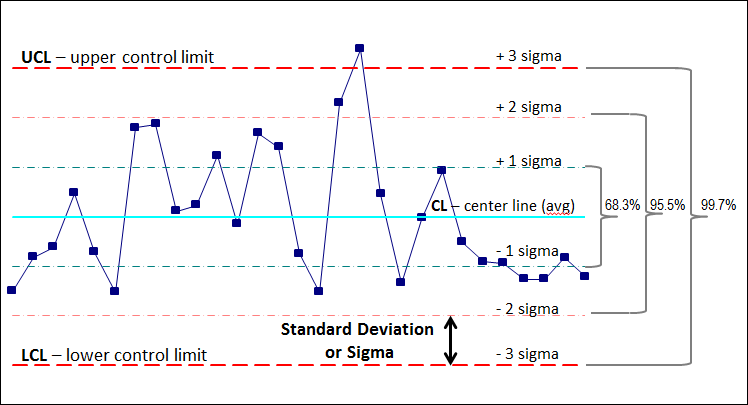
Statistical Course of Management (SPC) is a strong instrument for monitoring and bettering processes. One of many key charts utilized in SPC is the p-chart, designed to watch the proportion of nonconforming items in a pattern. Understanding the p-chart’s management limits is essential for successfully decoding the chart and making knowledgeable choices about course of stability. This text delves deep into the p-chart management limits components, its derivation, software, and the concerns concerned in its sensible use.
What’s a p-Chart?
A p-chart is a management chart used to watch the proportion (p) of faulty or nonconforming objects in a pattern. In contrast to the x-bar and R charts which monitor steady knowledge, the p-chart focuses on attribute knowledge – knowledge that may be categorised as both conforming or nonconforming, good or unhealthy, go or fail. Every pattern represents a subgroup of things drawn from the method, and the proportion of defectives in every pattern is plotted on the chart. The p-chart then makes use of management limits to find out if the method is working inside its anticipated variation or if it is exhibiting uncommon patterns indicative of instability.
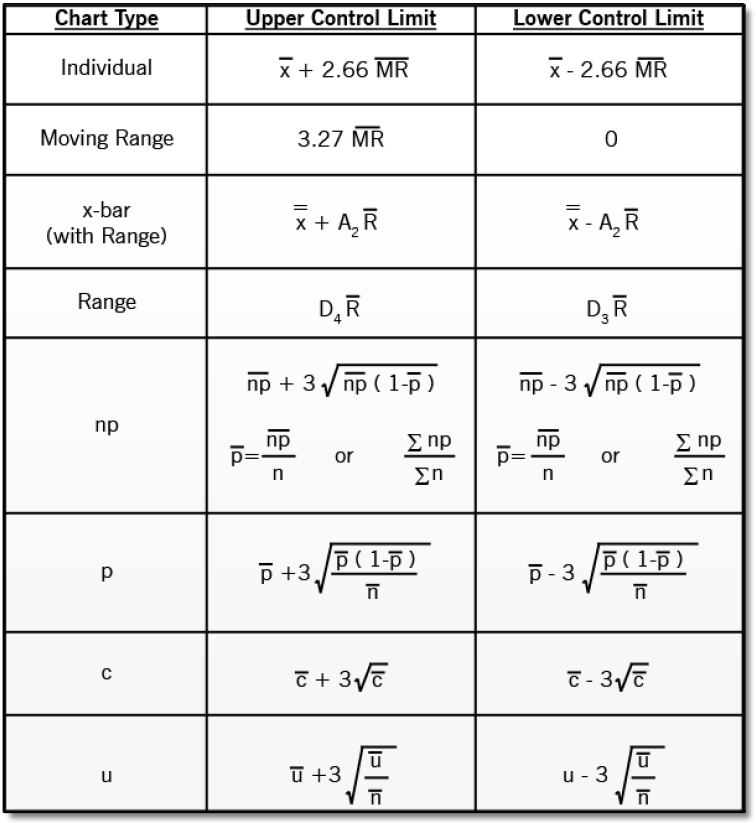
The p-Chart Management Limits System: A Detailed Breakdown
The management limits for a p-chart are calculated based mostly on the typical proportion of defectives and the variability inherent within the course of. The formulation are:
-
Middle Line (CL): p̄ That is the typical proportion of defectives throughout all samples. It is calculated as:
p̄ = Σpi / ok
the place:
- p̄ is the typical proportion of defectives
- Σpi is the sum of the proportions of defectives in every pattern (i = 1, 2, …, ok)
- ok is the variety of samples
-
Higher Management Restrict (UCL): p̄ + 3√(p̄(1-p̄)/n) This restrict represents the higher boundary of acceptable variation. Exceeding this restrict suggests the method could also be uncontrolled.
-
Decrease Management Restrict (LCL): p̄ – 3√(p̄(1-p̄)/n) This restrict represents the decrease boundary of acceptable variation. Falling beneath this restrict additionally suggests potential course of instability.
the place:
- n is the pattern dimension (variety of objects in every pattern)
Derivation of the p-Chart Management Limits
The formulation are derived from the binomial distribution, which fashions the likelihood of observing a sure variety of successes (defectives) in a set variety of trials (pattern dimension). For giant pattern sizes, the binomial distribution could be approximated by the conventional distribution, permitting for the usage of the 3-sigma limits. The usual deviation of the proportion of defectives is given by:
σp = √(p̄(1-p̄)/n)
The three-sigma limits are then calculated by including and subtracting 3 times the usual deviation from the typical proportion:
UCL = p̄ + 3σp = p̄ + 3√(p̄(1-p̄)/n)
LCL = p̄ – 3σp = p̄ – 3√(p̄(1-p̄)/n)
The selection of 3-sigma limits is a conference, providing a stability between sensitivity to actual course of shifts and minimizing false alarms. Different multiples of the usual deviation can be utilized, however 3-sigma is essentially the most broadly accepted.
Sensible Concerns and Functions
The profitable implementation of a p-chart depends on a number of essential components:
-
Pattern Dimension (n): The pattern dimension needs to be giant sufficient to offer an inexpensive estimate of the proportion of defectives. Smaller pattern sizes result in wider management limits and lowered sensitivity to course of shifts. A typical rule of thumb is to have not less than 5 defectives in every pattern.
-
Pattern Choice: Samples needs to be consultant of the method and randomly chosen to keep away from bias. Systematic sampling or biased choice can result in inaccurate conclusions.
-
Rational Subgrouping: Samples needs to be grouped rationally to seize potential variations throughout the course of. For example, samples is perhaps taken from the identical machine, operator, or shift.
-
Course of Stability: The p-chart assumes the method is steady when it is being arrange. If the method will not be steady initially, will probably be tough to interpret the management chart. Preliminary knowledge needs to be rigorously examined for outliers and tendencies earlier than developing the chart.
-
Dealing with LCL < 0: In some instances, significantly when p̄ is low or n is giant, the calculated LCL could be adverse. Since a proportion can’t be adverse, the LCL is usually set to 0 in such conditions.
-
Decoding the Chart: Factors outdoors the management limits point out potential course of instability. Examine these factors to determine the foundation reason for the variation. Patterns throughout the management limits (e.g., tendencies, cycles) additionally counsel potential points that want consideration.
Examples and Illustrations:
Let’s contemplate an instance: A producing course of produces widgets, and samples of 100 widgets are inspected day by day. Over 20 days, the variety of faulty widgets in every pattern is recorded: 5, 3, 7, 4, 6, 2, 8, 5, 4, 3, 6, 5, 7, 4, 2, 3, 6, 5, 4, 8.
-
Calculate p̄: The sum of faulty widgets is 94. Subsequently, p̄ = 94 / (20 * 100) = 0.047.
-
Calculate UCL and LCL:
UCL = 0.047 + 3√(0.047(1-0.047)/100) ≈ 0.099
LCL = 0.047 – 3√(0.047(1-0.047)/100) ≈ -0.005 (Since LCL < 0, set LCL = 0) -
Plot the information: Plot the proportion of defectives for every day on the chart with the middle line at 0.047, UCL at 0.099, and LCL at 0.
This instance demonstrates how you can calculate and use the p-chart management limits. Any factors above 0.099 would counsel a major enhance within the proportion of defectives, requiring speedy investigation.
Past the Primary p-Chart:
Whereas the usual p-chart is broadly used, variations exist to deal with particular conditions:
-
p-chart with variable pattern sizes: When pattern sizes range from subgroup to subgroup, a modified components is used to calculate the management limits. This includes calculating the typical pattern dimension and adjusting the usual deviation accordingly.
-
c-chart: If the pattern dimension is fixed, a c-chart, which displays the variety of defectives reasonably than the proportion, is perhaps extra acceptable.
-
u-chart: If the pattern dimension varies and the variety of defectives is monitored, a u-chart (items of defects per unit) is used.
Conclusion:
The p-chart is a beneficial instrument for monitoring the proportion of nonconforming objects in a course of. Understanding the p-chart management limits components and its underlying assumptions is essential for efficient software. By rigorously choosing pattern sizes, making certain consultant sampling, and accurately decoding the chart, organizations can use the p-chart to determine course of instability, scale back defects, and enhance general high quality. Nevertheless, it’s important to keep in mind that the p-chart is only one instrument in a broader high quality administration system, and its effectiveness is dependent upon a holistic strategy to course of enchancment. Combining the p-chart with different SPC strategies and root trigger evaluation strategies will result in extra complete and efficient high quality management.

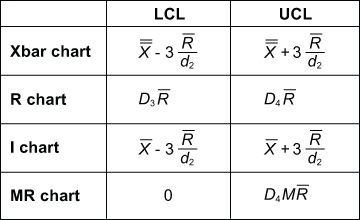



:max_bytes(150000):strip_icc()/ThreeSigmaLimits_final-3e323eac8e104e09a15fb5ca9e8b264a.png)
Closure
Thus, we hope this text has supplied beneficial insights into Understanding and Making use of the p-Chart Management Limits System: A Complete Information. We thanks for taking the time to learn this text. See you in our subsequent article!
