Understanding And Using The T-Desk Chart (PDF And Past)

Understanding and Using the t-Desk Chart (PDF and Past)

Associated Articles: Understanding and Using the t-Desk Chart (PDF and Past)

Introduction

With enthusiasm, let’s navigate by means of the intriguing subject associated to Understanding and Using the t-Desk Chart (PDF and Past). Let’s weave fascinating data and supply contemporary views to the readers.

Understanding and Using the t-Desk Chart (PDF and Past)

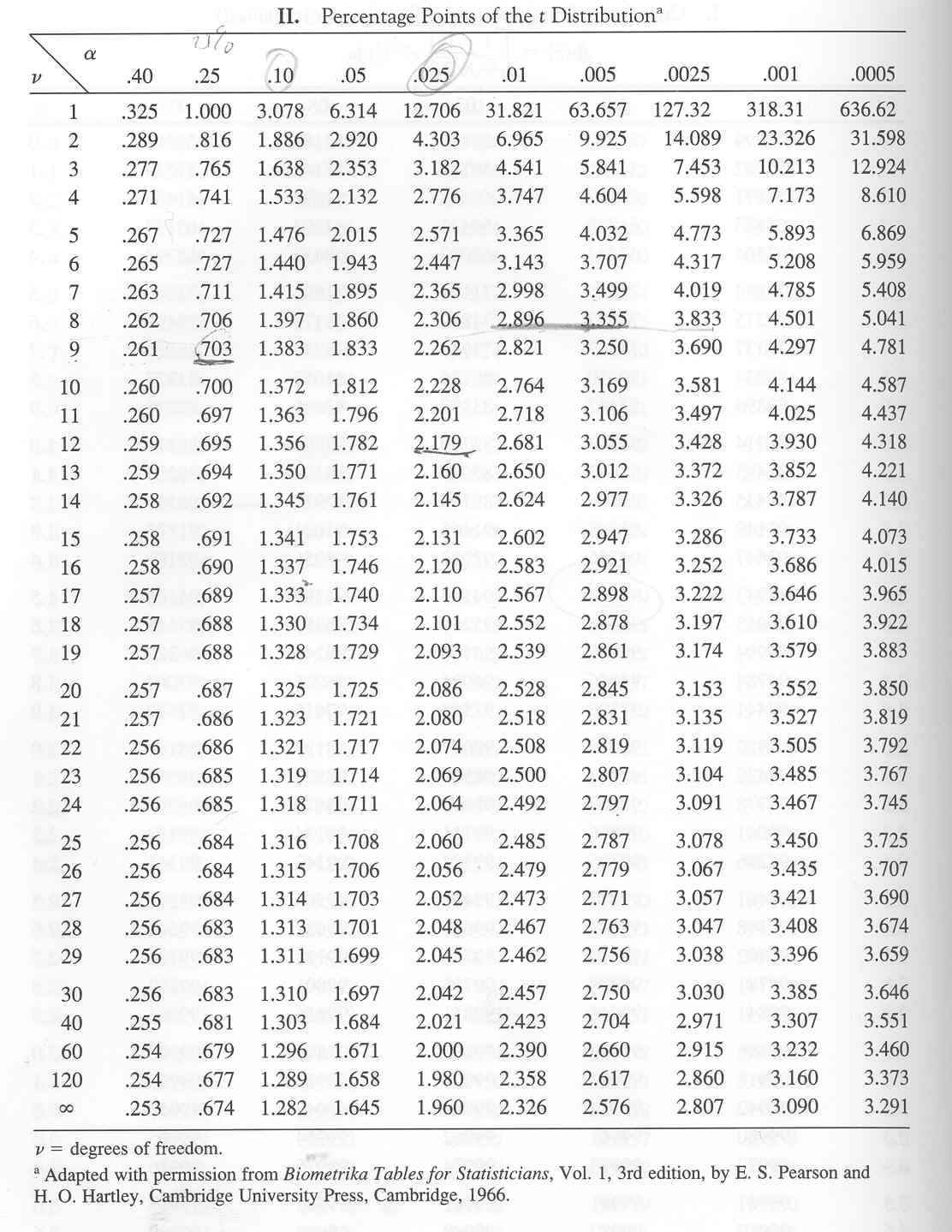
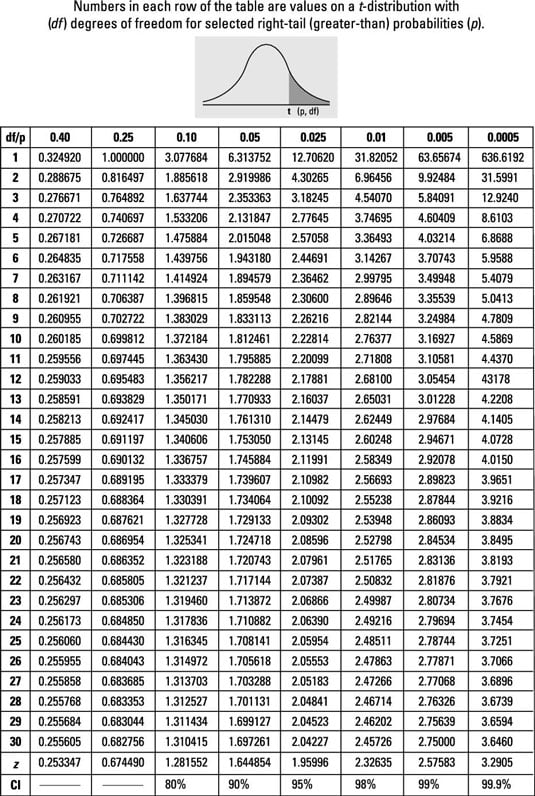
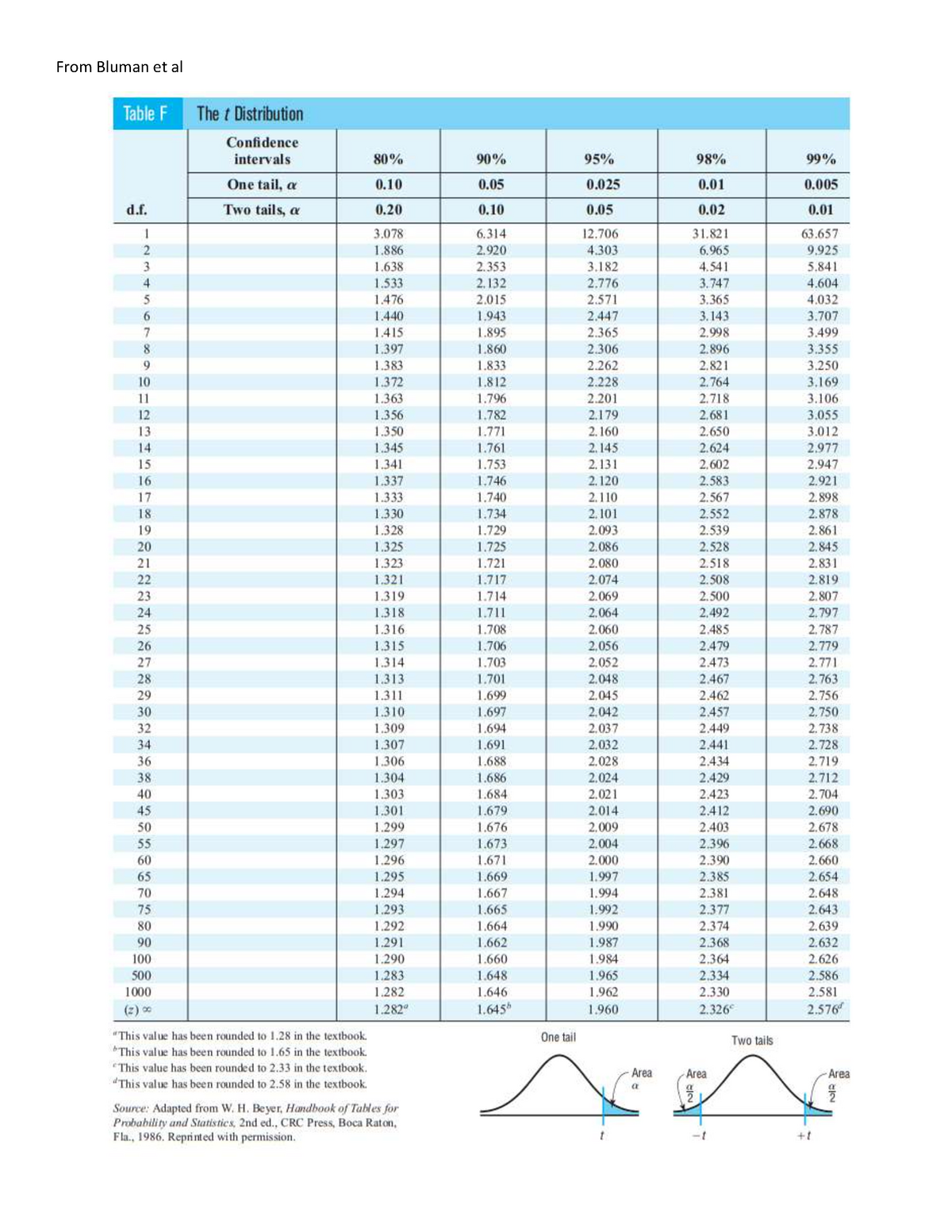
The t-table, also referred to as the Scholar’s t-distribution desk, is a vital device in statistics used to find out vital values for speculation testing and setting up confidence intervals when the inhabitants customary deviation is unknown. In contrast to the z-table, which depends on the traditional distribution, the t-table accounts for the added uncertainty launched by estimating the inhabitants customary deviation from a pattern. This text supplies a complete overview of the t-table, its purposes, the way to interpret it, and the provision of t-table charts in PDF format together with different strategies for accessing and using this important statistical useful resource.

The Essence of the t-Distribution:

The t-distribution, developed by William Sealy Gosset underneath the pseudonym "Scholar," is a chance distribution that resembles the traditional distribution however has heavier tails. Which means it assigns extra chance to excessive values in comparison with the traditional distribution. This attribute is especially essential when coping with smaller pattern sizes, the place the pattern customary deviation is a much less exact estimate of the inhabitants customary deviation. Because the pattern measurement will increase, the t-distribution converges in the direction of the traditional distribution.

The form of the t-distribution is decided by its levels of freedom (df), which is calculated as df = n - 1, the place ‘n’ represents the pattern measurement. A bigger pattern measurement (and therefore bigger levels of freedom) leads to a t-distribution that extra intently approximates the traditional distribution.

Decoding the t-Desk:

A typical t-table is organized as a matrix with rows representing levels of freedom (df) and columns representing totally different significance ranges (alpha ranges). The importance degree (α) represents the chance of rejecting the null speculation when it’s truly true (Sort I error). Widespread significance ranges are 0.10, 0.05, 0.025, 0.01, and 0.005. The values inside the desk signify the vital t-values.

To make use of the t-table:

1. Decide the levels of freedom (df): Calculate df = n – 1, the place ‘n’ is your pattern measurement.
2. Choose the importance degree (α): That is decided by the specified confidence degree and the kind of speculation check being carried out (one-tailed or two-tailed). A 95% confidence interval corresponds to a 0.05 significance degree for a two-tailed check and 0.025 for a one-tailed check.
3. Find the intersection: Discover the row akin to your levels of freedom and the column akin to your chosen significance degree. The worth at this intersection is the vital t-value.

Functions of the t-Desk:

The t-table is indispensable in numerous statistical purposes:

• One-Pattern t-test: This check compares the imply of a single pattern to a identified or hypothesized inhabitants imply.
• Two-Pattern t-test (Impartial Samples): This check compares the technique of two unbiased teams to find out if there is a statistically important distinction between them. This check may be additional divided into equal variance and unequal variance t-tests, relying on whether or not the inhabitants variances are assumed to be equal.
• Paired t-test: This check compares the technique of two associated teams, comparable to measurements taken on the identical topics earlier than and after a remedy.
• Confidence Intervals: The t-table is used to calculate confidence intervals for the inhabitants imply when the inhabitants customary deviation is unknown. The margin of error is calculated utilizing the vital t-value.

Accessing t-Desk Charts in PDF Format:

Quite a few web sites and textbooks supply downloadable t-table charts in PDF format. A easy Google seek for "t-table pdf" will yield quite a few outcomes. These PDFs supply a handy offline reference, significantly helpful for college students and researchers who could not all the time have web entry. Nevertheless, it is essential to make sure the reliability of the supply. Respected statistical web sites or established textbooks are most popular sources.

Various Strategies for Accessing t-Values:

Whereas PDF t-tables are available, a number of different strategies supply larger flexibility and comfort:

• Statistical Software program Packages: Software program like SPSS, R, SAS, and Python (with libraries like SciPy) present features to instantly calculate t-values based mostly on the levels of freedom and significance degree. This eliminates the necessity for handbook desk lookup and reduces the danger of errors.
• On-line Calculators: Many web sites supply on-line t-value calculators. These calculators are user-friendly and supply immediate outcomes, eliminating the necessity to interpret a desk.
• Spreadsheet Software program: Spreadsheet packages like Microsoft Excel and Google Sheets additionally embody features (e.g., T.INV, T.INV.2T) for calculating t-values.

Understanding One-Tailed vs. Two-Tailed Assessments:

The selection between a one-tailed and a two-tailed check depends upon the analysis query.

• One-tailed check: This check examines whether or not the pattern imply is considerably larger than or considerably lower than the inhabitants imply. It is used when the analysis speculation specifies the route of the distinction. The importance degree (α) is concentrated in a single tail of the distribution.
• Two-tailed check: This check examines whether or not the pattern imply is considerably totally different from the inhabitants imply, with out specifying the route of the distinction. The importance degree (α) is cut up between each tails of the distribution.

The t-table must be interpreted in another way for one-tailed and two-tailed assessments. For a one-tailed check, use the column akin to the chosen α degree. For a two-tailed check, use the column akin to α/2.

Limitations of the t-Desk:

Whereas the t-table is a robust device, it has limitations:

• Assumption of Normality: The t-test assumes that the info is roughly usually distributed. For small pattern sizes, deviations from normality can considerably have an effect on the outcomes. In such instances, non-parametric assessments could also be extra acceptable.
• Independence of Observations: The t-test assumes that the observations are unbiased of one another. Violations of this assumption can result in inaccurate conclusions.
• Homogeneity of Variances (for two-sample t-tests): The unbiased samples t-test assumes that the inhabitants variances are equal (homoscedasticity). If this assumption is violated, a modified t-test or a non-parametric different ought to be thought-about.

Conclusion:

The t-table is a basic device in statistical inference, offering vital values for speculation testing and confidence interval development when coping with unknown inhabitants customary deviations. Whereas PDF variations supply a handy offline useful resource, using statistical software program or on-line calculators supplies larger accuracy, effectivity, and suppleness. Understanding the nuances of the t-distribution, levels of freedom, significance ranges, and the excellence between one-tailed and two-tailed assessments is essential for the proper interpretation and software of the t-table. All the time take into account the assumptions underlying the t-test to make sure the validity of the outcomes. By mastering using the t-table and its alternate options, researchers and college students can confidently analyze information and draw significant conclusions.

Closure

Thus, we hope this text has supplied precious insights into Understanding and Using the t-Desk Chart (PDF and Past). We thanks for taking the time to learn this text. See you in our subsequent article!